搜索
【题目】若关于x的一元二次方程（x﹣2）（x﹣3）=m有实数根x1、x2，且x1＜x2，则下列结论中错误的是（ ）.
A. 当m=0时，x1=2，x2=3
B. m＞﹣
C. 当m＞0时，2＜x1＜x2＜3
D. 二次函数y=（x﹣x1）（x﹣x2）+m的图象与x轴交点的坐标为（2，0）和（3，0）
参考答案：
【答案】C
【解析】试题分析：根据方程的解的定义可以判定A正确；根据二次函数的最值问题，且结合题意可以判定B正确；根据二次函数与x轴交点的有关性质可以判定C错误；根据二次函数的定义可以判定D正确．①∵m=0时，方程为（x﹣2）（x﹣3）=0，∴x1=2，x2=3，故A正确；②设y=（x﹣2）（x﹣3）=x2﹣5x+6=（x﹣
）2﹣
，∴y的最小值为﹣
，∵一元二次方程（x﹣2）（x﹣3）=m有实数根x1、x2，且x1＜x2，∴m＞﹣
，故B正确；③∵m＞O时，y=（x﹣2）（x﹣3）＞0，函数y′=（x﹣2）（x﹣3）﹣m与x轴交于（x1，0），（x2，0），∴x1＜2＜3＜X2，故C错误；④∵y=（x﹣x1）（x﹣x2）+m=（x﹣2）（x﹣3）﹣m+m=（x﹣2）（x﹣3），∴函数与x轴交于点（2，0），（3，0）．故D正确．故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD内接于⊙O，AC平分∠BAD,延长DC交AB的延长线于点E ．
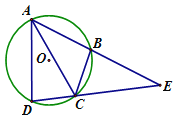
（1）若∠ADC=86°，求∠CBE的度数；
（2）若AC=EC，求证：AD=BE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC的∠ABC和∠ACB的平分线BE，CF交于点G，若∠BGC=115°，则∠A= ．
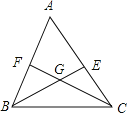
【答案】50°
【解析】
试题分析：根据三角形内角和定理求出∠GBC+∠GCB，根据角平分线的定义求出∠ABC+∠ACB，根据三角形内角和定理计算即可．
解：∵∠BGC=115°，
∴∠GBC+∠GCB=180°﹣115°=65°，
∵BE，CF是△ABC的∠ABC和∠ACB的平分线，
∴∠GBC=
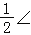ABC，∠G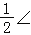CB=ACB，∴∠ABC+∠ACB=130°，
∴∠A=180°﹣130°=50°，
故答案为：50°．
【题型】填空题
【结束】
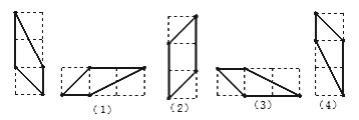
14【题目】如图所示，有（1）～（4）4个条形方格图，图中由实线围成的图形与前图全等的有
________（只要填序号即可）．
-
科目： 来源： 题型：
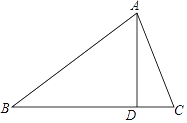
查看答案和解析>>【题目】在△ABC中，∠B=40°，AD是BC边上的高，且∠DAC=20°，则∠BAC=________．
【答案】70°
【解析】∵∠B=40°，AD⊥BC，
∴∠BAD=90°-40°=50°．
∵∠DAC=20°，
∴∠BAC=∠BAD+∠DAC=50°+20°=70°．
【题型】填空题
【结束】
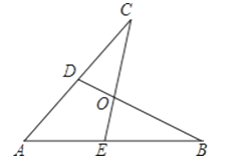
16【题目】如图所示，E，D是AB，AC上的两点，BD，CE交于点O，且AB=AC，使△ACE≌△ABD，你补充的条件是________
-
科目： 来源： 题型：
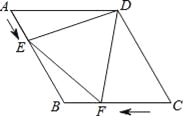
查看答案和解析>>【题目】如图，在菱形ABCD中，AB=4cm，∠ADC=120°，点E、F同时由A、C两点出发，分别沿AB、CB方向向点B匀速移动（到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF为等边三角形，则t的值为 ．
-
科目： 来源： 题型：
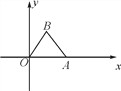
查看答案和解析>>【题目】如图，△OAB的OA边在x轴上，其中B点坐标为(3，4)且OB＝BA.
(1)求经过A，B，O三点的抛物线的解析式；
(2)将(1)中的抛物线沿x轴平移，设点A，B的对应点分别为点A′，B′，若四边形ABB′A′为菱形，求平移后的抛物线的解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC和△CDE都是等边三角形，则下列结论不成立的是（ ）
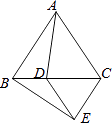
A.∠BDE=120°
B.∠ACE=120°
C.AB=BE
D.AD=BE
相关试题
