【题目】如图,将矩形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F,AD=12,DC=18.
(1)证明:△ADF≌△AB′E;
(2)求线段AF的长度.
(3)求△AEF的面积.

参考答案:
【答案】(1)见解析;(2)13;(3)78.
【解析】
(1)根据折叠的性质以及矩形的性质,运用ASA即可判定△ADF≌△AB′E;
(2)先设FA=FC=x,则DF=DC﹣FC=18﹣x,根据Rt△ADF中,AD2+DF2=AF2,即可得出方程122+(18﹣x)2=x2,然后解关于x的值即可;
(3)由S△AEF=![]() AEAD求解即可.
AEAD求解即可.
解:(1)∵四边形ABCD是矩形,
∴∠D=∠C=∠B′=90°,AD=CB=AB′,
∵∠DAF+∠EAF=90°,∠B′AE+∠EAF=90°,
∴∠DAF=∠B′AE,
在△ADF和△AB′E中, ,
,
∴△ADF≌△AB′E(ASA).
(2)由折叠性质得FA=FC,
设FA=FC=x,则DF=DC﹣FC=18﹣x,
在Rt△ADF中,AD2+DF2=AF2,
∴122+(18﹣x)2=x2.
解得x=13.
∵△ADF≌△AB′E(已证),
∴AE=AF=13,
(3)S△AEF=![]() ×12×13=78.
×12×13=78.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若
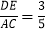 ,则
,则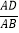 的值为( ).
的值为( ).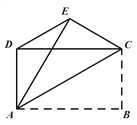
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形纸片的一角作折叠,使顶点
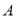 落在
落在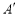 处,
处,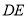 为折痕,将
为折痕,将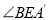 对折,使得
对折,使得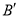 落在直线
落在直线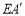 上,得折痕
上,得折痕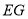 ,若
,若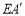 恰好平分
恰好平分 ,则
,则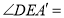 ___________
___________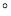 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( )
A.
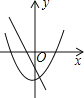 B.
B. 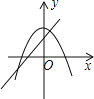 C.
C. 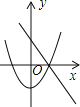 D.
D. 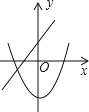
-
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)“校园手机”现象越来越受到社会的关注,小记者刘红随机调查了某校若干学生和家长对中学生带手机现象的看法,制作了如下的统计图:
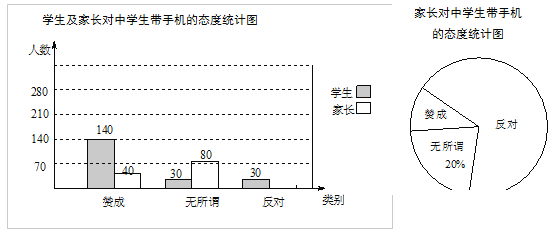
(1)求这次调查的总人数,并补全图1;
(2)求图2中表示家长“赞成”的圆心角的度数;
(3)针对随机调查的情况,刘红决定从初三一班表示赞成的4位家长中随机选择2位进行深入调查,其中包含小亮和小丁的家长,请你利用树状图或列表的方法,求出小亮和小丁的家长被同时选中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】自我国实施“限塑令”起,开始有偿使用环保购物袋,为了满足市场需求,某厂家生产A、B两种款式的布质环保购物袋,每天生产4500个,两种购物袋的成本和售价如下表,若设每天生产A种购物袋 x个.
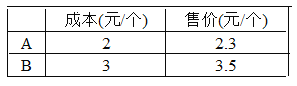
(1)用含x的整式表示每天的生产成本,并进行化简;
(2)用含x的整式表示每天获得的利润,并进行化简(利润=售价-成本);
(3)当x=1500时,求每天的生产成本与每天获得的利润.
相关试题

