【题目】下列说法:①已知直角三角形的面积为4,两直角边的比为1:2,则斜边长为![]() ;②直角三角形的最大边长为
;②直角三角形的最大边长为![]() ,最短边长为1,则另一边长为
,最短边长为1,则另一边长为![]() ;③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC为直角三角形;④等腰三角形面积为12,底边上的高为4,则腰长为5,其中正确结论的序号是( )
;③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC为直角三角形;④等腰三角形面积为12,底边上的高为4,则腰长为5,其中正确结论的序号是( )
A. 只有①②③ B. 只有①②④ C. 只有③④ D. 只有②③④
参考答案:
【答案】D
【解析】
①已知直角三角形的面积为4,两直角边的比为1:2,设两直角边的长度分别为x,2x,由此即可求出两直角边分别为2、4,然后根据勾股定理可以求出斜边,然后即可判断;
②直角三角形的最大边长为![]() ,最短边长为1,根据勾股定理可以求出另一边的长度,就可以判断是否正确;
,最短边长为1,根据勾股定理可以求出另一边的长度,就可以判断是否正确;
③在△ABC中,若∠A:∠B:∠C=1:5:6,根据三角形的内角和即可求出各个内角的度数,由此即可判断;
④由于等腰三角形面积为12,底边上的高为4,根据三角形的面积公式可以求出底边,再根据勾股定理即可求出腰长,然后即可判断是否正确.
①已知直角三角形的面积为4,两直角边的比为1:2,设两直角边的长度分别为x,2x,∴x2=4,∴两直角边分别为2、4,∴斜边为2![]() ,所以选项错误;
,所以选项错误;
②∵直角三角形的最大边长为![]() ,最短边长为1,∴根据勾股定理得第三边为
,最短边长为1,∴根据勾股定理得第三边为![]() ,故选项正确;
,故选项正确;
③在△ABC中,若∠A:∠B:∠C=1:5:6,∴∠A=15°,∠B=75°,∠C=90°,故选项正确;
④∵等腰三角形面积为12,底边上的高为4,∴底边=2×12÷4=6,底边的一半为3,∴腰长=5,故选项正确.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B和线段CD都在数轴上,点A、C、D、B起始位置所表示的数分别为-2、0、3、12;线段CD沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒.
(1)用含有t的代数式表示AC的长为多少,当t=2秒时,AC的长为多少.
(2)当0<t<9时AC+BD等于多少,当t>9时AC+BD等于多少.
(3)若点A与线段CD同时出发沿数轴的正方向移动,点A的速度为每秒2个单位,在移动过程中,是否存在某一时刻使得AC=2BD,若存在,请直接写出t的值;若不存在,请说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从A地向南偏东m°(0<m<90)的方向行走到B地,然后向左转30°行走到C地,则下面表述中,正确的个数是( )
①B可能在C的北偏西m°方向;
②当m<60时,B在C的北偏西(m+30)°方向;
③B不可能在C的南偏西m°方向;
④当m>60时,B在C的南偏西(150-m)°方向
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
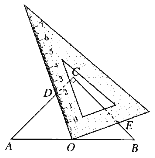
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,边AC的长为
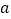 ,将一块边长足够大的三角板的直角顶点放在点O处,将三角板绕点O旋转,始终保持三角板的一条直角边与 AC相交,交点为点D,另一条直角边与BC相交,交点为点E.证明:等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值
,将一块边长足够大的三角板的直角顶点放在点O处,将三角板绕点O旋转,始终保持三角板的一条直角边与 AC相交,交点为点D,另一条直角边与BC相交,交点为点E.证明:等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值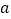 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K-∠H=33°,则∠K=__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】中学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查 B. 该校只有360个家长持反对态度
C. 样本是360个家长 D. 该校约有90%的家长持反对态度
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 O是△ABC外接圆的圆心,若⊙O的半径为5,∠A=45°,则
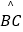 的长是( )
的长是( )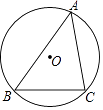
A. π
π
B.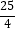 π
π
C. π
π
D. π
π
相关试题

