【题目】已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.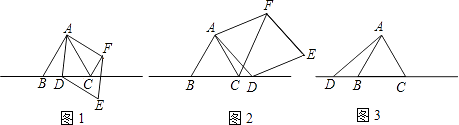
(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.
参考答案:
【答案】
(1)
证明:∵菱形AFED,
∴AF=AD,
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°=∠DAF,
∴∠BAC﹣∠DAC=∠DAF﹣∠DAC,
即∠BAD=∠CAF,
∵在△BAD和△CAF中
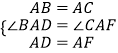 ,
,
∴△BAD≌△CAF,
∴CF=BD,
∴CF+CD=BD+CD=BC=AC,
即①BD=CF,②AC=CF+CD
(2)
解:AC=CF+CD不成立,AC、CF、CD之间存在的数量关系是AC=CF﹣CD,
理由是:由(1)知:AB=AC=BC,AD=AF,∠BAC=∠DAF=60°,
∴∠BAC+∠DAC=∠DAF+∠DAC,
即∠BAD=∠CAF,
∵在△BAD和△CAF中
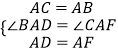 ,
,
∴△BAD≌△CAF,
∴BD=CF,
∴CF﹣CD=BD﹣CD=BC=AC,
即AC=CF﹣CD
(3)
AC=CD﹣CF.理由是:
∵∠BAC=∠DAF=60°,
∴∠DAB=∠CAF,
∵在△BAD和△CAF中
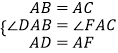 ,
,
∴△BAD≌△CAF(SAS),
∴CF=BD,
∴CD﹣CF=CD﹣BD=BC=AC,
即AC=CD﹣CF.
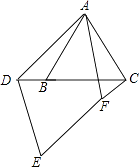
【解析】(1)根据已知得出AF=AD,AB=BC=AC,∠BAC=∠DAF=60°,求出∠BAD=CAF,证△BAD≌△CAF,推出CF=BD即可;(2)求出∠BAD=∠CAF,根据SAS证△BAD≌△CAF,推出BD=CF即可;(3)画出图形后,根据SAS证△BAD≌△CAF,推出CF=BD即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(1,5),B(3,﹣1)两点,在x轴上取一点M,使AM﹣BM取得最大值时,则M的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】生活中,有人喜欢把传送的便条折成“
 ”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):
”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):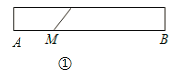

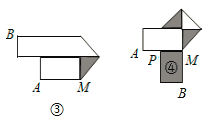
如果由信纸折成的长方形纸条(图①)长为2 6 厘米,分别回答下列问题:
(1)如果长方形纸条的宽为2厘米,并且开始折叠时起点M与点A的距离为3厘米,那么在图②中,BE=_____厘米; 在图④中,BM=______厘米.
(2)如果长方形纸条的宽为x厘米,现不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(结果用x表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.
例如:由图1可得到(a+b)=a+2ab+b.



图1 图2 图3
(1)写出由图2所表示的数学等式:_____________________;写出由图3所表示的数学等式:_____________________;
(2)利用上述结论,解决下面问题:已知a+b+c=11,bc+ac+ab=38,求a+b+c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,E是AB的中点,以点E为圆心,EB为半径画弧,交BC于点D,连接ED并延长到点F,使DF=DE,连接FC,若∠B=70°,则∠F的度数是( )

A. 40 B. 70 C. 50 D. 45
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果方程x2+px+q=0的两个根是x1 , x2 , 那么x1+x2=﹣p,x1x2=q,请根据以上结论,解决下列问题:
(1)已知关于x的方程x2+mx+n=0,(n≠0),求出一个一元二次方程,使它的两个根分别是已知方程两根的倒数;
(2)已知a、b满足a2﹣15a﹣5=0,b2﹣15b﹣5=0,求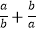 的值;
的值;
(3)已知a、b、c满足a+b+c=0,abc=16,求正数c的最小值. -
科目: 来源: 题型:
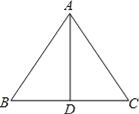
查看答案和解析>>【题目】如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是__.
①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB﹣BD=AC﹣CD.
相关试题

