【题目】已知,如图,直线y= ![]() x﹣4与x轴,y轴分别交于B、A,将该直线绕A点顺时针旋转α,且tanα=
x﹣4与x轴,y轴分别交于B、A,将该直线绕A点顺时针旋转α,且tanα= ![]() ,旋转后与x轴交于C点.
,旋转后与x轴交于C点.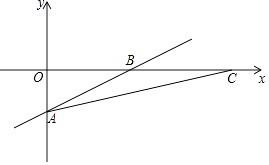
(1)求A、B、C的坐标;
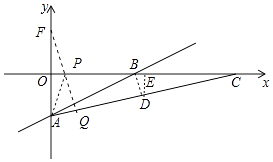
(2)在x轴上找一点P,使有一动点能在最短的时间内从点A出发,沿着A﹣P﹣C的运动到达C点,并且在AP上以每秒2个单位的速度移动,在PC上以每秒 ![]() 个单位移动,试用尺规作图找到P点的位置(不写作法,保留作图痕迹),并求出所用的最短时间t.
个单位移动,试用尺规作图找到P点的位置(不写作法,保留作图痕迹),并求出所用的最短时间t.
参考答案:
【答案】
(1)
解:∵直线y= ![]() x﹣4与x轴,y轴分别交于B、A,
x﹣4与x轴,y轴分别交于B、A,
∴A(0,﹣4),B(8,0),
过B作BD⊥AB交AC于D,过D作DE⊥x轴于E,则△AOB∽△BED
∴ ![]() =
= ![]() =
= ![]() ,
,
∵OA=4,OB=8,∠BAD=α,tanα= ![]() =
= ![]() ,
,
∴BE=1,DE=2
∴D(9,﹣2)∴直线AC解析式为y= ![]() x﹣4
x﹣4
∴C(18,0)
(2)
解:过点(0,4)作AC的垂线垂足为Q,该垂线与x轴的交点即为P点.
设点F(0,4),则A、F关于x轴对称,所以AP=FP,
∵S△ACF= ![]() AFOC=
AFOC= ![]() ACFQ,AF=8,OC=18,AC=
ACFQ,AF=8,OC=18,AC= ![]() =
= ![]() =2
=2 ![]() ,
,
∴FQ= ![]() ,
,
∵△CQP∽△COA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t= ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() ,
,
∵FQ是垂线段,
∴点P就是所求的点,此时动点能在最短的时间内从点A出发,沿着A﹣P﹣C的运动到达C点,
∴t= ![]()
![]() .
.
【解析】(1)过B作BD⊥AB交AC于D,过D作DE⊥x轴于E,则△AOB∽△BED,得到 ![]() =
= ![]() =
= ![]() ,求出点D坐标,求出AC的解析式即可求出点C坐标.(2)过点(0,4)作AC的垂线垂足为Q,该垂线与x轴的交点即为P点.设点F(0,4),则A、F关于x轴对称,所以AP=FP,首先证明t=
,求出点D坐标,求出AC的解析式即可求出点C坐标.(2)过点(0,4)作AC的垂线垂足为Q,该垂线与x轴的交点即为P点.设点F(0,4),则A、F关于x轴对称,所以AP=FP,首先证明t= ![]() ,由此推出
,由此推出
点P就是所求的点,此时动点能在最短的时间内从点A出发,沿着A﹣P﹣C的运动到达C点,求出FQ的长即可解决问题.
【考点精析】掌握一次函数的图象和性质是解答本题的根本,需要知道一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面两个圆圈分别表示负数集合和整数集合,请在这两个圆圈内各填入六个数,其中有三个数既在负数集合内,又在整数集合内.这三个数应填在哪里?你能说出这两个圆圈的重叠部分表示什么数的集合吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列性质中,菱形具有但矩形不一定具有的是( )
A.对边相等
B.对边平行
C.对角相等
D.对角线互相垂直 -
科目: 来源: 题型:
查看答案和解析>>【题目】与一条已知直线垂直的直线有( )
A. 1条 B. 2条 C. 3条 D. 无数条
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:5a﹣3a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小李某天的运营全是在东西走向的人民大街进行的,如果规定向东为正,向西为负,他这天下午的行车里程如下(单位:km)
+10、-3、-8、+11、-10、+12、+4、-15、-16、+15
(1)将最后一名乘客送到目的地时,小李距下午出车地点的距离是多少?
(2)若汽车的耗油量为0.5L/㎞,那么这天下午汽车共耗油多少?
-
科目: 来源: 题型:
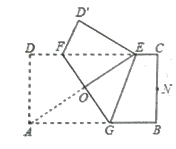
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AD= 1,AB一2.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点仪当触ED的外接圆与BC相切于BC的中点N.则折痕FG的长为________
相关试题

