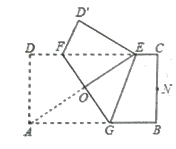
【题目】如图,矩形纸片ABCD中,AD= 1,AB一2.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点仪当触ED的外接圆与BC相切于BC的中点N.则折痕FG的长为________
参考答案:
【答案】![]()
【解析】试题解析:设AE与FG的交点为O.
根据轴对称的性质,得AO=EO.
取AD的中点M,连接MO.
则MO=![]() DE,MO∥DC.
DE,MO∥DC.
设DE=x,则MO=![]() x,
x,
在矩形ABCD中,∠C=∠D=90°,
∴AE为△AED的外接圆的直径,O为圆心.
延长MO交BC于点N,则ON∥CD.
∴∠CNM=180°-∠C=90°.
∴ON⊥BC,四边形MNCD是矩形.
∴MN=CD=AB=2.∴ON=MN-MO=2-![]() x.
x.
∵△AED的外接圆与BC相切,
∴ON是△AED的外接圆的半径.
∴OE=ON=2-![]() x,AE=2ON=4-x.
x,AE=2ON=4-x.
在Rt△AED中,AD2+DE2=AE2,
∴12+x2=(4-x)2.
解这个方程,得x=![]() .
.
∴DE=![]() ,OE=2-
,OE=2-![]() x=
x=![]() .
.
根据轴对称的性质,得AE⊥FG.
∴∠FOE=∠D=90°.可得FO=![]() .
.
又AB∥CD,∴∠EFO=∠AGO,∠FEO=∠GAO.
∴△FEO≌△GAO.∴FO=GO.
∴FG=2FO=![]() .
.
∴折痕FG的长是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,直线y=
 x﹣4与x轴,y轴分别交于B、A,将该直线绕A点顺时针旋转α,且tanα=
x﹣4与x轴,y轴分别交于B、A,将该直线绕A点顺时针旋转α,且tanα=  ,旋转后与x轴交于C点.
,旋转后与x轴交于C点.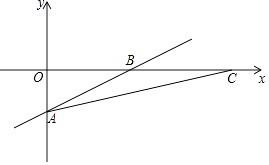
(1)求A、B、C的坐标;
(2)在x轴上找一点P,使有一动点能在最短的时间内从点A出发,沿着A﹣P﹣C的运动到达C点,并且在AP上以每秒2个单位的速度移动,在PC上以每秒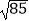 个单位移动,试用尺规作图找到P点的位置(不写作法,保留作图痕迹),并求出所用的最短时间t.
个单位移动,试用尺规作图找到P点的位置(不写作法,保留作图痕迹),并求出所用的最短时间t. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:5a﹣3a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小李某天的运营全是在东西走向的人民大街进行的,如果规定向东为正,向西为负,他这天下午的行车里程如下(单位:km)
+10、-3、-8、+11、-10、+12、+4、-15、-16、+15
(1)将最后一名乘客送到目的地时,小李距下午出车地点的距离是多少?
(2)若汽车的耗油量为0.5L/㎞,那么这天下午汽车共耗油多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣(﹣4)3等于( )
A.﹣12
B.12
C.﹣64
D.64 -
科目: 来源: 题型:
查看答案和解析>>【题目】若将代数式中的任意两个字母互换,代数式不变,则称这个代数式为完全对称式,如
 就是完全对称式.下列三个代数式:
就是完全对称式.下列三个代数式:①
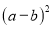 ;②
;② ;③
;③ .其中是完全对称式的是( ).
.其中是完全对称式的是( ).A. ①② B. ①③ C. ②③ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】(p﹣q)4÷(q﹣p)3=( )
A.p﹣q
B.﹣p﹣q
C.q﹣p
D.p+q
相关试题

