搜索
【题目】如图，已知EC∥AB，∠EDA=∠ABF．
（1）求证：四边形ABCD是平行四边形；
（2）求证：
=OEOF．
参考答案：
【答案】（1）证明见解析；（2）证明见解析．
【解析】
试题分析：（1）由EC∥AB，∠EDA=∠ABF，可证得∠DAB=∠ABF，即可证得AD∥BC，则得四边形ABCD为平行四边形；
（2）由EC∥AB，可得
，由AD∥BC，可得
，等量代换得出
，即
=OEOF．
试题解析：（1）∵EC∥AB，∴∠EDA=∠DAB，∵∠EDA=∠ABF，∴∠DAB=∠ABF，∴AD∥BC，∵DC∥AB，∴四边形ABCD为平行四边形；
（2）∵EC∥AB，∴△OAB∽△OED，∴，∵AD∥BC，∴△OBF∽△ODA，∴，∴，∴=OEOF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将抛物线y＝2x向右平移4个单位，再向上平移3个单位，得到的图象的表达式为( )
A. y＝2(x－4)＋3B. y＝2(x＋4)＋3C. y＝2(x－4)－3D. y＝2(x＋4)－3
-
科目： 来源： 题型：
查看答案和解析>>【题目】在边长为1的小正方形网格中，△AOB的顶点均在格点上．
（1）B点关于y轴的对称点坐标为 ；
（2）将△AOB向左平移3个单位长度得到△A1O1B1，请画出△A1O1B1；
（3）在（2）的条件下，A1的坐标为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计，发现每天销售量y（千克）与销售价x（元/千克）存在一次函数关系，如图所示．
（1）求y关于x的函数关系式（不要求写出x的取值范围）；
（2）应怎样确定销售价，使该品种苹果的每天销售利润最大？最大利润是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某检修站，甲组乘一辆汽车，从A地出发，沿东西方向的公路检修线路，约定向东为正，到收工时，行走记录为（单位：千米）：15，+5，－10，+10，－10，+4，
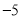，+1．同时，乙组也从A地出发，沿南北方向的公路检修线路，约定向北为正，到收工时，行走记录为（单位：千米）：－10，+9，+6， 
， 
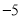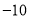，+4，＋6， 
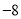．（1）分别计算收工时，甲、乙两组各在A地的哪一边，分别距A地多远？ （2）若每千米汽车耗油
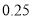升，求出发到收工时两组各耗油多少升？ -
科目： 来源： 题型：
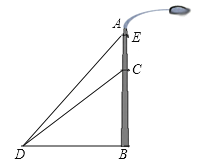
查看答案和解析>>【题目】如图，一垂直于地面的灯柱AB被一钢筋CD固定，CD与地面成45°夹角（∠CDB=45°），在C点上方2米处加固另一条钢线ED，ED与地面成53°夹角（∠EDB=53°），那么钢线ED的长度约为多少米？（结果精确到1米，参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知∠AOB=α，在射线OA、OB上分别取点OA1=OB1，连结A1B1，在B1A1、B1B上分别取点A2、B2，使B1B2=B1A2，连结A2B2…按此规律下去，记∠A2B1 B2=θ1，∠A3B2B3=θ2，…，∠An+1Bn Bn+1=θn，则θ2016﹣θ2015的值为（ ）
A.
B. 
C. 
D.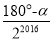 
相关试题
