【题目】如图,正方形ABCD的边长为2,E在正方形外,![]() ,过D作
,过D作![]() 于H,直线DH,EC交于点M,直线CE交直线AD于点,则下列结论正确的是( )
于H,直线DH,EC交于点M,直线CE交直线AD于点,则下列结论正确的是( )
①![]() ;②
;②![]() ;③
;③![]() ;④若PD=3AD,则MD=
;④若PD=3AD,则MD=![]()
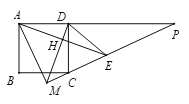
A.1个B.2个C.3个D.4个
参考答案:
【答案】C
【解析】
根据正方形的性质,利用全等的判定和性质、相似的判定和性质、垂直平分线的判定性质、勾股定理等知识对四个结论一一判断即可.
在正方形ABCD中,
AD=DC,
∵DE=DC,
∴AD=DE,
∴∠DAE=∠DEA,
∴①正确;
∵AD=DE,DH⊥AE,
∴DM是AE的垂直平分线,
∴AM=EM,
∴△AMD≌△EMD,
∴∠MAD=∠MED,
∵DE=DC,
∴∠DCE=∠MED,
∴∠MAD=∠DCE,
即∠MAH+∠DAH=∠DME+∠CDM
∵∠DAH+∠ADH=90°,
∠CDM+∠ADH=90°,
∴∠DAH=∠CDM,
∴∠MAH=∠DME,
∵AM=EM,
∴∠MAH=∠MEH,
∴∠DME=∠MEH,
∵DH⊥AE,
∴∠DME=∠MEH=45°,
故②正确;
在EP上截取EN=MC,则△DCM≌△DEN,
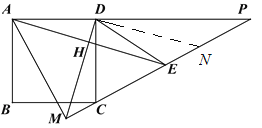
∴∠DNM=∠DME=45°,
∴△DMN是等腰直角三角形,
∴![]() ,
,
∵MN=ME+EN=AM+MC,
∴![]() ,
,
故③正确;
∵PD=3AD,AD=2,
∴PD=6,PA=8,
∵DM是AE的垂直平分线,
且∠DME=45°,
∴∠AMP=90°,
∴△PDC∽△PMA,
∴![]() ,
,
在Rt△PDC中, PC=![]() =2
=2![]() ,
,
在Rt△PAM中,AM=![]() ,PM=
,PM=![]() ,
,
∴CM=![]() ,
,
∵![]() ,
,
∴DM=![]() =
=![]() .
.
故④错误.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,过对角线
中,过对角线 上一点
上一点 作
作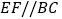 ,
, ,且
,且 ,
, ,则
,则 ( )
( )
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】妈妈在超市购买两种优质水果.先购买了2千克甲水果和3千克乙水果,共花费90元;后又购买了1千克甲水果和2千克乙水果,共花费55元.(每次两种水果的售价都不变)
(1)求甲水果和乙水果的售价分别是每千克多少元;
(2)如果还需购买两种水果共12千克,要求乙水果的数量不少于甲水果数量的2倍,请设计一种购买方案,使所需总费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,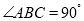 ,F是 AB 延长线上一点,
,F是 AB 延长线上一点,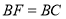 ,
,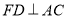 于点 D,交 BC 于点E.
于点 D,交 BC 于点E.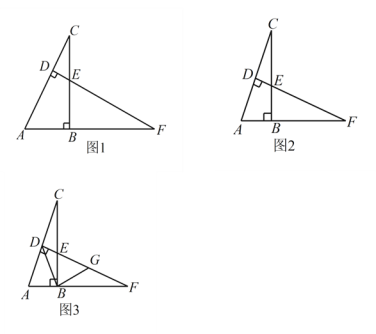
(1)如图1,求证:
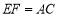 ;
;(2)如图2,若点
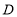 是
是 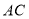 边的中点,求
边的中点,求 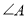 的度数;
的度数;(3)如图3,在(2)的条件下,连接
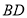 ,作
,作 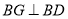 ,交
,交 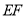 于点G,若
于点G,若 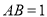 ,
, .求
.求  的面积
的面积 -
科目: 来源: 题型:
查看答案和解析>>【题目】若实数m、n满足等式
 ,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______.
,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校要开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整的统计图.
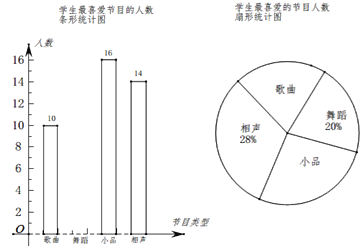
请你根据图中信息,回答下列问题:
(1)求本次调查的学生人数,并补全条形统计图;
(2)在扇形统计图中,求“歌曲”所在扇形的圆心角的度数;
(3)若该学校共有学生2000人,请问该学校大约有多少同学最喜爱“小品”节目?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”.比赛项目为:
 .唐诗;
.唐诗; .宋词;
.宋词; .论语;
.论语; .三字经.比赛形式分“单人组”和“双人组”.
.三字经.比赛形式分“单人组”和“双人组”.(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则小红和小明都没有抽到“论语”的概率是多少?请用画树状图或列表的方法进行说明.
相关试题

