【题目】如图,在 ![]() 中,
中,![]() ,F是 AB 延长线上一点,
,F是 AB 延长线上一点,![]() ,
,![]() 于点 D,交 BC 于点E.
于点 D,交 BC 于点E.
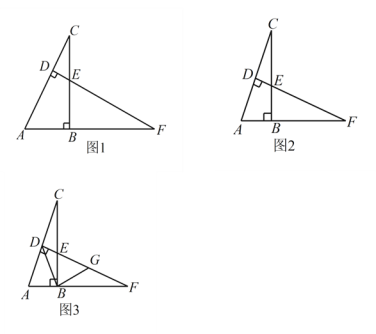
(1)如图1,求证:![]() ;
;
(2)如图2,若点 ![]() 是
是 ![]() 边的中点,求
边的中点,求 ![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,连接 ![]() ,作
,作 ![]() ,交
,交 ![]() 于点G,若
于点G,若 ![]() ,
,![]() .求
.求 ![]() 的面积
的面积
参考答案:
【答案】(1)详见解析;(2)67.5°;(3)![]() .
.
【解析】
(1)先证明三角形全等,利用全等性质即可解出此题
(2)连接CF,得出等腰Rt△BCF,由此得出角度关系,根据D又是中点DF⊥AC可以得出△AFC为等腰三角形,则DF就为角平分线,因此可以得出角度关系,联合求解即可.
(3)先证出△BCD≌△BFG,再证出△ABC≌△EBF,从而得出BEG和BEF的关系即可.
(1)证明:
∵FD⊥AC
∴∠ADF=90°
∵∠ABC=90°
∴∠ADF=∠ABC=∠EBF
∵∠C+∠A=∠F+∠A=90°
∴∠C=∠F
在△ABC和△EBF中
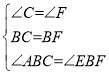
∴△ABC≌△EBF
∴AC=EF
(2)
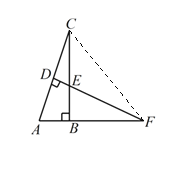
连接CF
∵点D是AC中点
∴AD=CD
∵FD⊥AC
∴∠ADF=∠CDF=90°
在△ADF和△CDF中
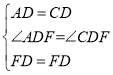
∴△ADF≌△CDF
∴∠AFD=∠CFD
∵BF=BC,BC⊥BF
∴△BCF是等腰直角三角形
∴∠BFC=∠BCF=∠AFD+∠CFD=45°
∴∠AFD=∠CFD=22.5°
∴∠A=90°-∠AFD=90°-22.5°=67.5°
(3)∵BG⊥BD
∴∠DBG=90°
∴∠DBC+∠EBG=∠FBG+∠EBG=90°
∴∠DBC=∠FBG
在△BCD和△BFG中
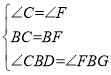
∴△BCD≌△BFG
∴CD=FG
∵CD=AD,AC=EF
∴FG=EG
∵△ABC≌△EBF
∴AB=BE=1
∴BF=BC=BE+CE=1+![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )

A.
 B. 2
B. 2 -
- C. 2
C. 2 -
- D. 4
D. 4 -
-
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,过对角线
中,过对角线 上一点
上一点 作
作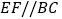 ,
, ,且
,且 ,
, ,则
,则 ( )
( )
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】妈妈在超市购买两种优质水果.先购买了2千克甲水果和3千克乙水果,共花费90元;后又购买了1千克甲水果和2千克乙水果,共花费55元.(每次两种水果的售价都不变)
(1)求甲水果和乙水果的售价分别是每千克多少元;
(2)如果还需购买两种水果共12千克,要求乙水果的数量不少于甲水果数量的2倍,请设计一种购买方案,使所需总费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,E在正方形外,
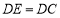 ,过D作
,过D作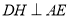 于H,直线DH,EC交于点M,直线CE交直线AD于点,则下列结论正确的是( )
于H,直线DH,EC交于点M,直线CE交直线AD于点,则下列结论正确的是( )①
 ;②
;②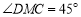 ;③
;③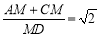 ;④若PD=3AD,则MD=
;④若PD=3AD,则MD=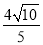
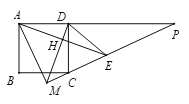
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若实数m、n满足等式
 ,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______.
,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校要开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整的统计图.
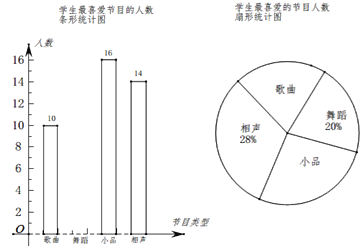
请你根据图中信息,回答下列问题:
(1)求本次调查的学生人数,并补全条形统计图;
(2)在扇形统计图中,求“歌曲”所在扇形的圆心角的度数;
(3)若该学校共有学生2000人,请问该学校大约有多少同学最喜爱“小品”节目?
相关试题

