【题目】近日,崂山区教体局对参加2018年崂山区禁毒知识竞赛的2500名初中学生的初试成绩(成绩均为整数)进行一次抽样调查,所得数据如下表:
成绩分组 | 60.5~70.5 | 70.5~80.5 | 80.5~90.5 | 90.5~100.5 |
频数 | 50 | 150 | 200 | 100 |
(1)抽取样本的总人数;
(2)根据表中数据,补全图中频数分布直方图;
(3)若规定初试成绩在90分以上(不包括90分)的学生进入决赛,则全区进入决赛的初中学生约有多少人.

参考答案:
【答案】(1)500;(2)见解析;(3)500
【解析】
(1)把表中的频数相加即为抽取样本的总人数;
(2)根据表中数据,补全图中频数分布直方图;
(3)用样本中成绩在90分以上(不包括90分)所占百分比去估计总体.
解:(1)抽取样本的容量=50+150+200+100=500;
(2)根据表中数据,补全图中频数分布直方图;
(3)若规定初试成绩在90分以上(不包括90分)的学生进入决赛,则全县进入决赛的学生约为2500×![]() =500人.
=500人.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠ABC=∠ACB,D为射线CB上一点(不与C、B重合),点E为射线CA上一点,∠ADE=∠AED.设∠BAD=α,∠CDE=β.
(1)如图(1),
①若∠BAC=40°,∠DAE=30°,则α= ,β= .
②写出α与β的数量关系,并说明理由;
(2)如图(2),当D点在BC边上,E点在CA的延长线上时,其它条件不变,写出α与β的数量关系,并说明理由.
(3)如图(3),D在CB的延长线上,根据已知补全图形,并直接写出α与β的关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径作⊙O,过点A作⊙O的切线AC,连结BC,交⊙O于点D,点E是BC边的中点,连结AE.
(1)求证:∠AEB=2∠C;
(2)若AB=6,
 ,求DE的长.
,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形纸片ABCD中,AB=3,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则图中重叠部分的面积为_____.
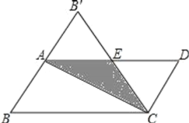
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆超市配送车从仓库O出发,向东走了4.5km到达超市A,继续走0.5km到达超市B,然后向西走9.5km到达超市C,最后回到仓库O.解答下列问题:
(1)以仓库O为原点,以向东为正方向,用1个单位长度表示1km,在所给的直线上画出数轴,并在数轴上表示出A、B、C的位置.
(2)结合数轴计算:超市C在超市A的什么方向,距超市A多远?
(3)若该配送车每千米耗油0.1升,在这次送货回仓过程中共耗油多少升?
解:(1)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=60°,BC=3厘米,AC=4厘米,点P从点B出发,沿B→C→A以每秒1厘米的速度匀速运动到点A.设点P的运动时间为x秒,B、P两点间的距离为y厘米.

小新根据学习函数的经验,对函数
 随自变量
随自变量 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.下面是小新的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x(s)
0
1
2
3
4
5
6
7
y(cm)
0
1.0
2.0
3.0
2.7
2.7
m
3.6
经测量m的值是(保留一位小数).
(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:在曲线部分的最低点时,在△ABC中画出点P所在的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2bx﹣3的对称轴为直线x=2.
(1)求b的值;
(2)在y轴上有一动点P(0,m),过点P作垂直y轴的直线交抛物线于点A(x1,y1),B(x2,y2),其中x1<x2.
①当x2﹣x1=3时,结合函数图象,求出m的值;
②把直线PB下方的函数图象,沿直线PB向上翻折,图象的其余部分保持不变,得到一个新的图象W,新图象W在0≤x≤5时,﹣4≤y≤4,求m的取值范围.

相关试题

