【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
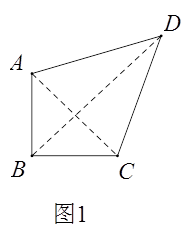
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,
①若AB=CD=1,AB//CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD.
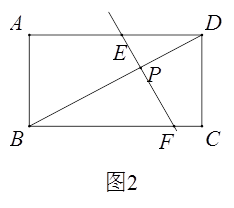
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形.求AE的长.
参考答案:
【答案】
(1)
解:①因为AB=CD=1,AB//CD,
所以四边形ABCD是平行四边形.
又因为AB=BC,
所以□ABCD是菱形.
又因为∠ABC=90度,
所以菱形ABCD是正方形.
所以BD= ![]() .
.
②如图1,连结AC,BD,
因为AB=BC,AC⊥BD,
所以∠ABD=∠CBD,
又因为BD=BD,
所以△ABD△CBD,
所以AD=CD.
(2)
解:若EF与BC垂直,则AE≠EF,BF≠EF,
所以四边形ABFE不是等腰直角四边形,不符合条件;
若EF与BC不垂直,
①当AE=AB时,如图2,
此时四边形ABFE是等腰直角四边形.
所以AE=AB=5.
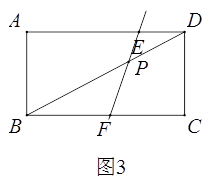
②当BF=AB时,如图3,
此时四边形ABFE是等腰直角四边形.
所以BF=AB=5,
因为DE//BF,
所以△PED~△PFB,
所以DE:BF=PD:PB=1:2,
所以AE=9-2.5=6.5.
综上所述,AE的长为5或6.5.
【解析】(1)①由AB=CD=1,AB//CD,根据“有一组对边平行且相等的四边形是平行四边形”可得四边形ABCD是平行四边形.由邻边相等AB=BC,有一直角∠ABC=90度,所以菱形ABCD是正方形.则BD= ![]() ;②连结AC,BD,由AB=BC,AC⊥BD,可知四边形ABCD是一个筝形,则只要证明△ABD△CBD,即可得到AD=CD.(2)分类讨论:若EF与BC垂直,明示有AE≠EF,BF≠EF,即EF与两条邻边不相等;由∠A=∠ABC=90°,可分类讨论AB=AE时,AB=BF时去解答.
;②连结AC,BD,由AB=BC,AC⊥BD,可知四边形ABCD是一个筝形,则只要证明△ABD△CBD,即可得到AD=CD.(2)分类讨论:若EF与BC垂直,明示有AE≠EF,BF≠EF,即EF与两条邻边不相等;由∠A=∠ABC=90°,可分类讨论AB=AE时,AB=BF时去解答.
【考点精析】解答此题的关键在于理解平行四边形的判定的相关知识,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
-
科目: 来源: 题型:
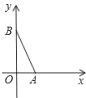
查看答案和解析>>【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,AC=AD,请增加一个条件,使△ABC≌△AED,你添加的条件是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为为50m.设饲养室长为x(m),占地面积为y(m2).

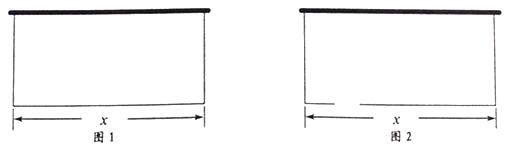
(1)如图1,问饲养室长x为多少时,占地面积y最大?
(2)如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大。小敏说:“只要饲养室长比(1)中的长多2m就行了.” -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
x+8与x轴,y轴分别交于点A和B,M是OB上的一点,若将△ABM沿AM折叠,点B恰好落在x轴上的点B′处,则直线AM的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形 对.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.

(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°,那么α=°,β=°.②求α,β之间的关系式.
(2)是否存在不同于以上②中的α,β之间的关系式?若存在,请求出这个关系式(求出一个即可);若不存在,说明理由.
相关试题

