【题目】如图,在同心⊙O中,大圆的半径为5,大圆的弦AB与小圆交于CD,AB=8,CD=3. 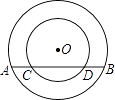
(1)求AC的长;
(2)求小圆的半径.
参考答案:
【答案】
(1)解:
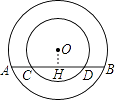
过O作OH⊥AB于H,
∵OH过O,OH⊥AB,AB=8,CD=3,
∴AH=BH=4,CH=DH= ![]() ,
,
∴AC=BD= ![]() (AB﹣CD)=
(AB﹣CD)= ![]() ;
;
(2)解:连接OA和OD,

∵OA=5,AH=4,
∴由勾股定理得:OH=3,
∵HD= ![]() ,
,
∴由勾股定理得:OD= ![]() =
= ![]() ,
,
即小圆的半径为 ![]() .
.
【解析】(1)过O作OH⊥AB于H,根据垂径定理求出AH=BH、CH=DH,即可求出答案;(2)连接OA、OD,根据勾股定理求出OH,根据勾股定理求出OD即可.
【考点精析】本题主要考查了垂径定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上,点D在⊙O上,连接CD,且CD=OA,OC=2
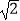 .求证:CD是⊙O的切线.
.求证:CD是⊙O的切线. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
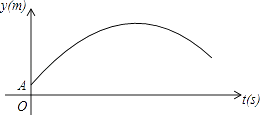
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形ECGF的边长分别为a和6,
(1) 写出表示阴影部分面积的代数式(结果要求化简);
(2) 求
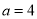 时,阴影部分的面积.
时,阴影部分的面积.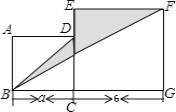
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,中线AD,BE交于F,则图中共有等腰三角形( )
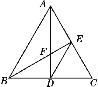
A. 3个 B. 4个 C. 5个 D. 6个
-
科目: 来源: 题型:
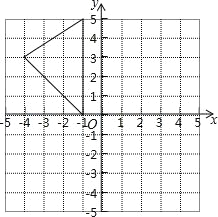
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A、B是数轴上的两个点,点A表示的数为13,点B表示的数为
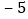 ,动点P从点B出发,以每秒4个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
,动点P从点B出发,以每秒4个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.(1)点P表示的数为__________(用含t的代数式表示);
(2)点P运动多少秒时,PB=2PA?
(3)若M为BP的中点,N为PA的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请直接写出线段MN的长.

相关试题

