【题目】(本题12分)如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF//AB交AC于F

(1)求证:AE=DF.
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
参考答案:
【答案】(1)详见解析;(2)平行四边形AEDF为菱形;理由详见解析
【解析】
试题(1)利用AAS推出△ADE≌△DAF,再根据全等三角形的对应边相等得出AE=DF;
(2)先根据已知中的两组平行线,可证四边形DEFA是,再利用AD是角平分线,结合AE∥DF,易证∠DAF=∠FDA,利用等角对等边,可得AE=DF,从而可证AEDF实菱形.
试题解析:(1)∵DE∥AC,∠ADE=∠DAF,
同理∠DAE=∠FDA,
∵AD=DA,
∴△ADE≌△DAF,
∴AE=DF;
(2)若AD平分∠BAC,四边形AEDF是菱形,
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴∠DAF=∠FDA.
∴AF=DF.
∴平行四边形AEDF为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,点F为对角线BD上一点,点E为AB的延长线上一点,DF=BE,CE=CF.求证:(1)△CFD≌△CEB;(2)∠CFE=60°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为_____.

-
科目: 来源: 题型:
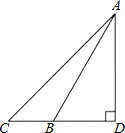
查看答案和解析>>【题目】如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )
A.2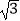 m
m
B.2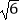 m
m
C.(2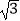 ﹣2)m
﹣2)m
D.(2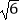 ﹣2)m
﹣2)m -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )
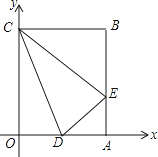
A.(3,1)
B.(3, )
)
C.(3, )
)
D.(3,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两地相距900km,一列快车从甲地开往乙地,一列慢车从乙地开往甲地,两车同时出发,行了4小时后两车相遇,快车的速度是慢车速度的2倍.
(1)请求出慢车与快车的速度?
(2)两车出发后多长时间,它们相距225千米?
-
科目: 来源: 题型:
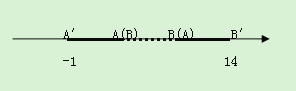
查看答案和解析>>【题目】(1)如图,在数轴上有一小木棒AB,若平移木棒,使B落在A处,则A′所表示的数为 -1,若将A落在B处时,则B′所表示的数14,它的两个端点A、B所表示的数分别是 、 .
(2)老师给东东出了一道关于年龄的数学题:我像你那么小时,你才两岁;你像我那么大时,我已经44岁了,你猜我有多少岁?亲爱的同学,你能不能利用上一题的方法帮助小东求出老师的年龄呢?
相关试题

