【题目】如图,有一个不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是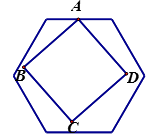
参考答案:
【答案】![]()
( ![]() )
)
【解析】解:因为AC为对角线,故当AC最小时,正方形边长此时最小.
①当 A、C都在对边中点时(如下图所示位置时),显然AC取得最小值,
∵正六边形的边长为1,
∴AC=![]() ,
,
∴a2+a2=AC2=![]() .
.
∴a=![]() =
=![]() .
.
②当正方形四个顶点都在正六边形的边上时,a最大(如下图所示).
设A′(t,![]() )时,正方形边长最大.
)时,正方形边长最大.
∵OB′⊥OA′.
∴B′(-![]() , t)
, t)
设直线MN解析式为:y=kx+b,M(-1,0),N(-![]() , -
, -![]() )(如下图)
)(如下图)
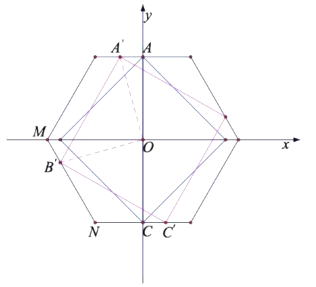
∴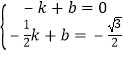 .
.
∴![]() .
.
∴直线MN的解析式为:y=![]() (x+1),
(x+1),
将B′(-![]() , t)代入得:t=
, t)代入得:t=![]() -
-![]() .
.
此时正方形边长为A′B′取最大.
∴a=![]() =3-
=3-![]() .
.
故答案为:![]() ≤a≤3-
≤a≤3-![]() .
.
分情况讨论.① 当A、C都在对边中点时,a最小.②当正方形四个顶点都在正六边形的边上时,a最大.根据题意求出正方形对角线的长度,再根据勾股定理即可求出a.从而得出a的范围.
-
科目: 来源: 题型:
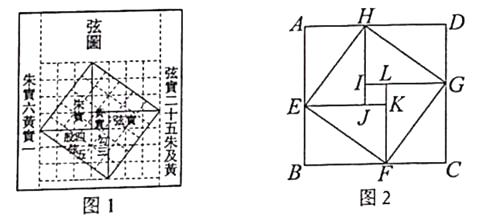
查看答案和解析>>【题目】我国三国时期数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图1所示.在图2中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ//AB,则正方形EFGH的边长为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则cos∠EFG的值为 .
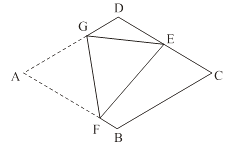
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:
(1)
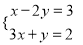 (2)
(2) 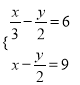
(3)
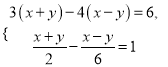 (4)
(4) 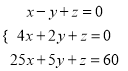
-
科目: 来源: 题型:
查看答案和解析>>【题目】电脑中有一种游戏——蜘蛛纸牌,开始游戏前有500分的基本分,游戏规则如下:①操作一次减x分;②每完成一列加y分.有一次小明在玩这种“蜘蛛纸牌”游戏时,随手用表格记录了两个时段的电脑显示:
第一时段
第二时段
完成列数
2
5
分数
634
898
操作次数
66
102
(1)通过列方程组,求x,y的值;
(2)如果小明最终完成此游戏(即完成10列),分数是1 182,问他一共操作了多少次?
-
科目: 来源: 题型:
查看答案和解析>>【题目】荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
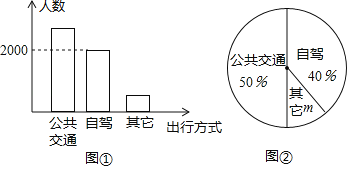
A. 本次抽样调查的样本容量是5000
B. 扇形图中的m为10%
C. 样本中选择公共交通出行的有2500人
D. 若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
相关试题

