【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
0<x≤200 | 0.48 |
200<x≤400 | 0.53 |
x>400 | 0.78 |
七月份是用电高峰期,李叔计划七月份电费支出不超过200元,直接写出李叔家七月份最多可用电的度数是( )
A. 100B. 396C. 397D. 400
参考答案:
【答案】B
【解析】
先判断出电费是否超过400度,然后根据不等关系:七月份电费支出不超过200元,列不等式计算即可.
解:0.48×200+0.53×200
=96+106
=202(元),
故七月份电费支出不超过200元时电费不超过400度,
依题意有0.48×200+0.53(x-200)≤200,
解得x≤396![]()
答:李叔家七月份最多可用电的度数是396.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别是BE,CD的中点,
(1)求证:△AMN是等边三角形.
(2)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx﹣8(a≠0)的对称轴是直线x=1,
(1)求证:2a+b=0;
(2)若关于x的方程ax2+bx﹣8=0,有一个根为4,求方程的另一个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )

A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1) 观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2) 若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a<0)的对称轴为x=1,交x轴的一个交点为(x1,0),且﹣1<x1<0,有下列5个结论:①abc>0;②9a﹣3b+c<0;③2c<3b;④(a+c)2<b2;⑤a+b>m(am+b)(m≠1的实数)其中正确的结论有( )
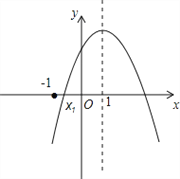
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).
(1)直接写出点A1,B1,C1的坐标.
(2)在图中画出△A1B1C1.
(3)连接AA1,求△AOA1的面积.

相关试题

