【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别是BE,CD的中点,
(1)求证:△AMN是等边三角形.
(2)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由.

参考答案:
【答案】(1)证明见解析;(2)CD=BE.理由见解析
【解析】试题分析:(1)由等边三角形的性质得到AB=AC,AE=AD, ∠BAC=∠EAD=60°,从而得到BE=CD, 再由中点的定义得到EN=DN, 即有AN=AM, 从而可以得到结论;
(2)可以利用SAS判定△ABE≌△ACD,全等三角形的对应边相等,所以CD=BE.
试题解析:解:(1)∵△ABC和△ADE是等边三角形,∴AB=AC,AE=AD, ∠BAC=∠EAD=60°,
∴AB-AE=AC-AD,即BE=CD, ∴M,N分别是BE,CD的中点,∴EM=![]() BE,DN=
BE,DN=![]() CD, ∴EN=DN, ∴EM+AE=DN+AD,即AN=AM, ∵∠BAC=60°, ∴△AMN是等边三角形;
CD, ∴EN=DN, ∴EM+AE=DN+AD,即AN=AM, ∵∠BAC=60°, ∴△AMN是等边三角形;
(2)CD=BE.理由如下:
∵△ABC和△ADE为等边三角形,∴AB=AC,AE=AD,∠BAC=∠EAD=60°.
∵∠BAE=∠BAC∠EAC=60°∠EAC,∠DAC=∠DAE∠EAC=60°∠EAC,∠BAE=∠DAC,∴△ABE≌△ACD,∴CD=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用长度一定的不锈钢材料设计成外观为矩形的框架(如图①②中的一种).设竖档AB=x米,请根据以上图案回答下列问题:(题中的不锈钢材料总长均指各图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行)
(1)在图①中,如果不锈钢材料总长度为12米,当x为多少时,矩形框架ABCD的面积为3平方米?
(2)在图②中,如果不锈钢材料总长度为12米,当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮从家步行到公交站台,等公交车去学校.图中折线表示小亮的行程
 与所花时间
与所花时间 之间的函数关系.下列说法:
之间的函数关系.下列说法: 他离家
他离家 共用了
共用了 ;
; 他等公交车的时间是
他等公交车的时间是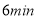 ;
; 他步行的速度是
他步行的速度是 ;
; 公交车的速度是
公交车的速度是 .正确的有________________(只填正确说法的序号).
.正确的有________________(只填正确说法的序号). 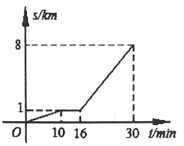
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx﹣8(a≠0)的对称轴是直线x=1,
(1)求证:2a+b=0;
(2)若关于x的方程ax2+bx﹣8=0,有一个根为4,求方程的另一个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )

A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(单位:度)
电费价格(单位:元/度)
0<x≤200
0.48
200<x≤400
0.53
x>400
0.78
七月份是用电高峰期,李叔计划七月份电费支出不超过200元,直接写出李叔家七月份最多可用电的度数是( )
A. 100B. 396C. 397D. 400
相关试题

