【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求一次函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C在x轴上,且△ABC的面积是8,求此时点C的坐标;
(3)反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)
(1≤x≤4)的图象记为曲线C1,将C1向右平移3个单位长度,得曲线C2,则C1平移至C2处所扫过的面积是_________.(直接写出答案)

参考答案:
【答案】(1)![]() ,
,![]() ;(2)点C的坐标为
;(2)点C的坐标为![]() 或
或![]() ;(3)27.
;(3)27.
【解析】试题分析:(1)由点A的坐标利用反比例函数图象上点的坐标特征即可求出a值,从而得出反比例函数解析式;由勾股定理得出OA的长度从而得出点B的坐标,由点A、B的坐标利用待定系数法即可求出直线AB的解析式;
(2)设点C的坐标为(m,0),令直线AB与x轴的交点为D,根据三角形的面积公式结合△ABC的面积是8,可得出关于m的含绝对值符号的一元一次方程,解方程即可得出m值,从而得出点C的坐标;
(3)设点E的横坐标为1,点F的横坐标为6,点M、N分别对应点E、F,根据反比例函数解析式以及平移的性质找出点E、F、M、N的坐标,根据EM∥FN,且EM=FN,可得出四边形EMNF为平行四边形,再根据平行四边形的面积公式求出平行四边形EMNF的面积S,根据平移的性质即可得出C1平移至C2处所扫过的面积正好为S.
试题解析:
(1)∵点A(4,3)在反比例函数y=![]() 的图象上,
的图象上,
∴a=4×3=12,
∴反比例函数解析式为y=![]() ;
;
∵OA=![]() =5,OA=OB,点B在y轴负半轴上,
=5,OA=OB,点B在y轴负半轴上,
∴点B(0,﹣5).
把点A(4,3)、B(0,﹣5)代入y=kx+b中,
得:![]() ,解得:
,解得:![]() ,
,
∴一次函数的解析式为y=2x﹣5.
(2)设点C的坐标为(m,0),令直线AB与x轴的交点为D,如图1所示.
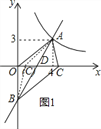
令y=2x﹣5中y=0,则x=![]() ,
,
∴D(![]() ,0),
,0),
∴S△ABC=![]() CD(yA﹣yB)=
CD(yA﹣yB)=![]() |m﹣
|m﹣![]() |×[3﹣(﹣5)]=8,
|×[3﹣(﹣5)]=8,
解得:m=![]() 或m=
或m=![]() .
.
故当△ABC的面积是8时,点C的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
(3)设点E的横坐标为1,点F的横坐为6,点M、N分别对应点E、F,如图2所示.
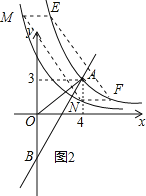
令y=![]() 中x=1,则y=12,
中x=1,则y=12,
∴E(1,12),;
令y=![]() 中x=4,则y=3,
中x=4,则y=3,
∴F(4,3),
∵EM∥FN,且EM=FN,
∴四边形EMNF为平行四边形,
∴S=EM(yE﹣yF)=3×(12﹣3)=27.
C1平移至C2处所扫过的面积正好为平行四边形EMNF的面积.
故答案为:27.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有
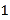 个,若从中随机摸出一个球,这个球是白球的概率为
个,若从中随机摸出一个球,这个球是白球的概率为 .
.(
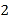 )请直接写出袋子中白球的个数.
)请直接写出袋子中白球的个数.(
 )随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AH⊥BC,垂足为H,若AB+BH=CH,∠ABH=80°,则∠BAC=_________ 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-3,2),B(-4,-3),C(-1,-1)。
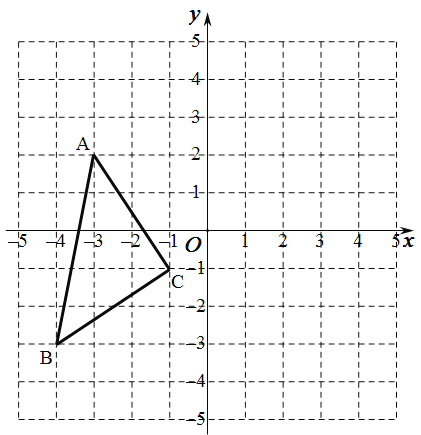
(1)写出△ABC关于x轴对称的△A1B1C1 的各顶点坐标;
(2)画出△ABC关于y轴对称的△A2B2C2;
(3)求△A2B2C2的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=
 ∠BAC=60°,于是
∠BAC=60°,于是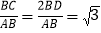 ;
;
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
(1)求证:△ADB≌△AEC;
(2)若AD=2,BD=3,请计算线段CD的长;
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
(3)证明:△CEF是等边三角形;
(4)若AE=4,CE=1,求BF的长.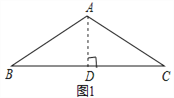


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ ABC中,AB=AC,点D在线段BC上,AD=BD,△ ADC是等腰三角形,求△ABC三个内角的度数。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线y=ax2+bx(a≠0)经过A(6,0)、B(8,8)两点.
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,在坐标平面内有点P,求出所有满足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).


相关试题

