【题目】对每个数位数字均不为零且互不相等的一个三位正整数![]() ,若将
,若将![]() 的十位数字与百位数字交换位置,得到一个新的三位数
的十位数字与百位数字交换位置,得到一个新的三位数![]() ,我们称
,我们称![]() 为
为![]() 的“置换数”,如:
的“置换数”,如:![]() 的“置效为“
的“置效为“![]() ”;若由
”;若由![]() 的百位、十位、个位上的数字任选两个组成一个新的两位数,所有新的两位数之和记为
的百位、十位、个位上的数字任选两个组成一个新的两位数,所有新的两位数之和记为![]() ,我们称
,我们称![]() 为
为![]() 的“行生数”.如
的“行生数”.如![]() :因为
:因为![]() 所以
所以![]() 的“衍生数”为
的“衍生数”为![]() .
.
(1)直接写出![]() 的“置换数”,并求
的“置换数”,并求![]() 的“衍生数”;
的“衍生数”;
(2)对每个数位数字均不为零且互不相等的一个三位正整数![]() ,设十位数字为
,设十位数字为![]() ,若
,若![]() 的“衍生数”与
的“衍生数”与![]() 的“置换数”之差为
的“置换数”之差为![]() ,求
,求![]() .
.
参考答案:
【答案】(1)897;528;(2)814
【解析】
(1)直接根据“置换数”和“衍生数”的定义解答即可;
(2)设x的百位数字为a,各位数字为b,根据![]() 的“衍生数”与
的“衍生数”与![]() 的“置换数”之差为
的“置换数”之差为![]() 列出关于a和b的二元一次方程,结合a和b是互不相等的正整数求解即可.
列出关于a和b的二元一次方程,结合a和b是互不相等的正整数求解即可.
(1)![]() 的“置换数”是:897,
的“置换数”是:897, ![]() 的“衍生数”是:98+97+89+87+78+79=528;
的“衍生数”是:98+97+89+87+78+79=528;
(2)设x的百位数字为a,各位数字为b,则 的“衍生数”是10+a+10+b+10a+1+10a+b+10b+1+10b+a=22a+22b+22;x 的“置换数”是100+10a+b,由题意得,
22a+22b+22-100-10a-b=102,
即4a+7b=60,
∵a和b是互不相等的正整数,
∴a=8,b=4,
∴x=814.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果商店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位;千克)
-3
-2
-1.5
0
1
2.5
筐数
1
4
2
3
2
8
(1)这20筐苹果中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,这20筐苹果总计超过或不足多少千克?
(3)若苹果每千克售价
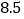 元,则出售这20筐苹果可卖多少元?
元,则出售这20筐苹果可卖多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B中心对称得C2,C2与x轴交于另一点C,将C2关于点C中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_________.
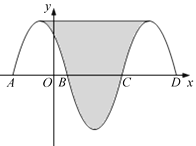
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,对角线AC、BD相交于O,EF过点O,连接AF、CE.
(1)求证:△BFO≌△DEO;
(2)若AF⊥BC,试判断四边形AFCE的形状,并加以证明;
(3)若在(2)的条件下再添加EF平分∠AEC,试判断四边形AFCE的形状,无需说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_____.

【答案】32
【解析】试题分析:∵抛物线y=﹣x2﹣2x+3与x轴交于点A、B,
∴当y=0时,则﹣x2﹣2x+3=0,
解得x=﹣3或x=1,
则A,B的坐标分别为(﹣3,0),(1,0),
AB的长度为4,
从C1,C3两个部分顶点分别向下作垂线交x轴于E、F两点.
根据中心对称的性质,x轴下方部分可以沿对称轴平均分成两部分补到C1与C2.
如图所示,阴影部分转化为矩形.
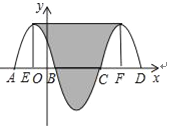
根据对称性,可得BE=CF=4÷2=2,则EF=8
利用配方法可得y=﹣x2﹣2x﹣3=﹣(x+1)2+4
则顶点坐标为(﹣1,4),即阴影部分的高为4,
S阴=8×4=32.
考点:抛物线与x轴的交点.
【题型】填空题
【结束】
17【题目】解方程:(1)2(3x﹣1)=16;(2)
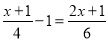 ;(3)
;(3)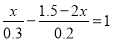 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
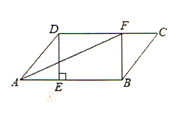
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

相关试题

