【题目】如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O. 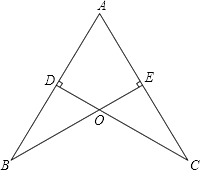
(1)求证:AD=AE;
(2)试猜想:OA与BC的位置关系,并加以证明.
参考答案:
【答案】
(1)证明:∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°,
△ACD和△ABE中,
∵ 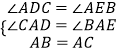
∴△ACD≌△ABE(AAS),
∴AD=AE
(2)猜想:OA⊥BC.
证明:连接OA、BC, 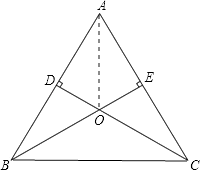
∵CD⊥AB,BE⊥AC,
∴∠ADC=∠AEB=90°.
在Rt△ADO和Rt△AEO中,
∵ ![]()
∴Rt△ADO≌Rt△AEO(HL).
∴∠DAO=∠EAO,
又∵AB=AC,
∴OA⊥BC.
【解析】(1)根据AAS推出△ACD≌△ABE,根据全等三角形的性质得出即可;(2)证Rt△ADO≌Rt△AEO,推出∠DAO=∠EAO,根据等腰三角形的性质推出即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售某一种新型通讯产品.已知每件产品的进价为4万元,每月销售该种产品的总开支(不含进价)总计11万元.在销售过程中发现,月销售量
 (件)与销售单价
(件)与销售单价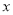 (万元)之间存在着如图所示的一次函数关系.
(万元)之间存在着如图所示的一次函数关系.
(1)求
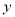 关于
关于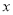 的函数关系式;(直接写出结果)
的函数关系式;(直接写出结果)(2)试写出该公司销售该种产品的月获利
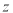 (万元)关于销售单价
(万元)关于销售单价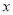 (万元)的函数关系式.当销售单价
(万元)的函数关系式.当销售单价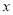 为何值时,月获利最大?并求这个最大值;
为何值时,月获利最大?并求这个最大值;(月获利=月销售额-月销售产品总进价-月总开支.)
(3)若公司希望该产品一个月的销售获利不低于5万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(3,4),C(4,﹣1).
(1)试在平面直角坐标系中,画出△ABC;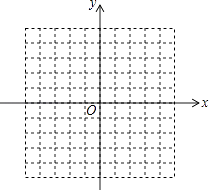
(2)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标;
(3)在x轴上找到一点P,使点P到点A、B两点的距离和最小;
(4)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在1,0,﹣2,﹣1中,最大的数是( )
A. 1 B. 0 C. ﹣2 D. ﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
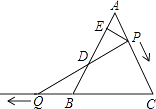
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值。
(1)已知x+y=15,x2+y2=113,求x2﹣xy+y2的值.
(2)先化简,再求值: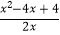 ÷
÷  +1,在0,1,2,三个数中选一个合适的,代入求值.
+1,在0,1,2,三个数中选一个合适的,代入求值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若单项式﹣3xnym与单项式4x4﹣nyn﹣1是同类项,则m+n的值是( )
A. 2 B. 3 C. 4 D. 5
相关试题

