【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(3,4),C(4,﹣1).
(1)试在平面直角坐标系中,画出△ABC; 
(2)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标;
(3)在x轴上找到一点P,使点P到点A、B两点的距离和最小;
(4)求△ABC的面积.
参考答案:
【答案】
(1)解:如图所示△ABC即为所求
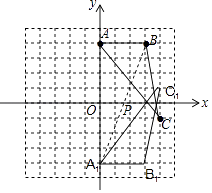
(2)解:A1(0,﹣4),B1(3,﹣4),C1(4,1)
(3)解:连接A1B交x轴于P,点P即为所求
(4)解:S△ABC= ![]() ×3×5=
×3×5= ![]()
【解析】(1)根据题意作出图形即可;(2)根据关于x轴对称的点的特点即可得到结果;(3)连接A1B交x轴于P即可得到结论;(4)根据三角形的面积公式即可得到结论.
【考点精析】本题主要考查了作轴对称图形和轴对称-最短路线问题的相关知识点,需要掌握画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
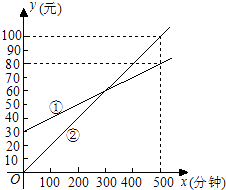
(1)有月租费的收费方式是(填①或②),月租费是元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面事件是随机事件的是( )
A.掷一枚硬币,出现反面
B.在标准大气压下,水加热到8℃时会沸腾
C.实数的绝对值不小于零
D.如果a,b是实数,那么ab=ba
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售某一种新型通讯产品.已知每件产品的进价为4万元,每月销售该种产品的总开支(不含进价)总计11万元.在销售过程中发现,月销售量
 (件)与销售单价
(件)与销售单价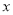 (万元)之间存在着如图所示的一次函数关系.
(万元)之间存在着如图所示的一次函数关系.
(1)求
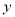 关于
关于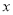 的函数关系式;(直接写出结果)
的函数关系式;(直接写出结果)(2)试写出该公司销售该种产品的月获利
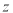 (万元)关于销售单价
(万元)关于销售单价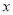 (万元)的函数关系式.当销售单价
(万元)的函数关系式.当销售单价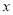 为何值时,月获利最大?并求这个最大值;
为何值时,月获利最大?并求这个最大值;(月获利=月销售额-月销售产品总进价-月总开支.)
(3)若公司希望该产品一个月的销售获利不低于5万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在1,0,﹣2,﹣1中,最大的数是( )
A. 1 B. 0 C. ﹣2 D. ﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O.
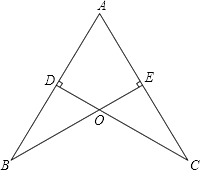
(1)求证:AD=AE;
(2)试猜想:OA与BC的位置关系,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
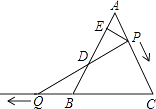
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
相关试题

