【题目】如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点. 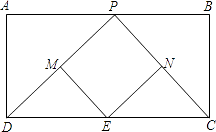
(1)求证:四边形PMEN是平行四边形;
(2)请直接写出当AP为何值时,四边形PMEN是菱形.
参考答案:
【答案】
(1)证明:∵M,E分别为PD,CD的中点,
∴ME∥PC,
同理可证:ME∥PD,
∴四边形PMEN为平行四边形
(2)解:当PA=5时,四边形PMEN为菱形.
理由:∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC,
∵AP=5,AB=CD=10,
∴AP=BP,
在△APD和△BPC中,
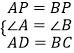 ,
,
∴△APD≌△BPC(SAS),
∴PD=PC,
∵M、N、E分别是PD、PC、CD的中点,
∴EN=PM= ![]() PD,PN=EM=
PD,PN=EM= ![]() PC,
PC,
∴PM=EM=EN=PN,
∴四边形PMEN是菱形
【解析】(1)由M、N、E分别是PD、PC、CD的中点,根据三角形中位线的性质,可证得ME∥PC,EN∥PD,继而证得四边形PMEN是平行四边形;(2)由AP=BP=5,可证得△APD≌△BPC(SAS),继而可得PD=PC,则可得PM=EM=EN=PN,继而证得四边形PMEN是菱形.
【考点精析】通过灵活运用平行四边形的判定和菱形的判定方法,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形即可以解答此题.
-
科目: 来源: 题型:
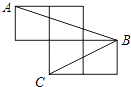
查看答案和解析>>【题目】如图,每个小正方形的边长为1,A、B、C为小正方形的顶点,求证:∠ABC=45°.
-
科目: 来源: 题型:
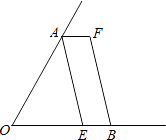
查看答案和解析>>【题目】如图,已知∠AOB,OA=OB,点E在OB上,且四边形AEBF是平行四边形,请你只用无刻度的直尺在图中画出∠AOB的平分线(保留画图痕迹,不写画法),并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售一种服装,进价120元/件,售价200元/件,公司对大量购买有优惠政策,凡是一次性购买20件以上的,每多买一件,售价就降低1元.设顾客购买
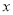 (件)时公司的利润为
(件)时公司的利润为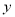 (元).
(元).(1)当一次性购买
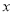 件
件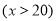 时,
时,①售价为 元/件;
②求
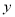 (元)与
(元)与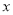 (件)之间的函数表达式
(件)之间的函数表达式在此优惠政策下,顾客购买多少件时公司能够获得最大利润?
(2) 设售价为
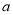 元/件,求
元/件,求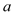 在什么范围内才能保证公司每次卖的越多,利润也越多.
在什么范围内才能保证公司每次卖的越多,利润也越多. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
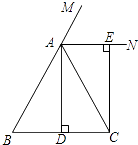
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】一款手机连续两次降价,价格由原来的1300元下降了468元,设平均每次降价的百分率为x,则可列方程为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000,4400000000这个数用科学记数法表示为( )
A.44×108
B.4.4×108
C.4.4×109
D.0.44×1010
相关试题

