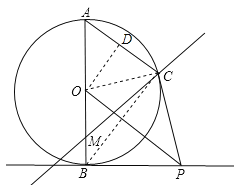
【题目】已知AB是⊙O的直径,PB是⊙O的切线,C是⊙O上的点,AC∥OP,M是直径AB上的动点,A与直线CM上的点连线距离的最小值为d,B与直线CM上的点连线距离的最小值为f.
(1)求证:PC是⊙O的切线;
(2)设OP=![]() AC,求∠CPO的正弦值;
AC,求∠CPO的正弦值;
(3)设AC=9,AB=15,求d+f的取值范围.

参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)9≤d+f≤15.
;(3)9≤d+f≤15.
【解析】试题分析:(1)连接OC,根据等腰三角形的性质得到∠A=∠OCA,由平行线的性质得到∠A=∠BOP,∠ACO=∠COP,等量代换得到∠COP=∠BOP,由切线的性质得到∠OBP=90°,根据全等三角形的性质即可得到结论;
(2)过O作OD⊥AC于D,根据相似三角形的性质得到CDOP=OC2,根据已知条件得到![]() =
=![]() ,由三角函数的定义即可得到结论;
,由三角函数的定义即可得到结论;
(3)连接BC,根据勾股定理得到BC的值,当M与A重合时,得到d+f=12,当M与B重合时,得到d+f=9,于是得到结论.
试题解析:解:(1)连接OC,∵OA=OC,∴∠A=∠OCA,∵AC∥OP,∴∠A=∠BOP,∠ACO=∠COP,∴∠COP=∠BOP,∵PB是⊙O的切线,AB是⊙O的直径,∴∠OBP=90°,在△POC与△POB中,∵OC=OB,∠COP=∠BOP,OP=OP,∴△COP≌△BOP,∴∠OCP=∠OBP=90°,∴PC是⊙O的切线;
(2)过O作OD⊥AC于D,∴∠ODC=∠OCP=90°,CD=![]() AC,∵∠DCO=∠COP,∴△ODC∽△PCO,∴
AC,∵∠DCO=∠COP,∴△ODC∽△PCO,∴![]() ,∴CDOP=OC2,∵OP=
,∴CDOP=OC2,∵OP=![]() AC,∴AC=
AC,∴AC=![]() OP,∴CD=
OP,∴CD=![]() OP,∴
OP,∴![]() OPOP=OC2,∴
OPOP=OC2,∴![]() =
=![]() ,∴sin∠CPO=
,∴sin∠CPO=![]() =
=![]() ;
;
(3)连接BC,∵AB是⊙O的直径,∴AC⊥BC,∵AC=9,AB=15,∴BC=![]() =12,当M与A重合时,d=0,f=AB=15,∴d+f=15,当M与B重合时,d=9,f=0,∴d+f=9,∴d+f的取值范围是:9≤d+f≤15.
=12,当M与A重合时,d=0,f=AB=15,∴d+f=15,当M与B重合时,d=9,f=0,∴d+f=9,∴d+f的取值范围是:9≤d+f≤15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
 中,
中,  ,垂足为点
,垂足为点 ,
,  ,垂足为点
,垂足为点 ,
,  为
为 边的中点,连结
边的中点,连结 、
、 、
、 .
.
(
 )猜想
)猜想 的形状,并说明理由.
的形状,并说明理由.(
 )若
)若 ,
,  ,求
,求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景
如图
 ,在正方形
,在正方形 的内部,作
的内部,作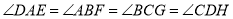 ,根据三角形全等的条件,易得
,根据三角形全等的条件,易得 ≌
≌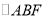 ≌
≌ ≌
≌ ,从而得到四边形
,从而得到四边形 是正方形.
是正方形.类比探究
如图
 ,在正
,在正 的内部,作
的内部,作 ,
,  ,
,  ,
,  两两相交于
两两相交于 ,
,  ,
,  三点(
三点( ,
,  ,
,  三点不重合).
三点不重合).(
 )
) ,
, 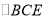 ,
,  是否全等?如果是,请选择其中一对进行证明.
是否全等?如果是,请选择其中一对进行证明.(
 )
)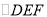 是否为正三角形?请说明理由.
是否为正三角形?请说明理由.(
 )进一步探究发现,图
)进一步探究发现,图 中的
中的 的三边存在一定的等量关系,设
的三边存在一定的等量关系,设 ,
, 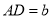 ,
,  ,请探索
,请探索 ,
,  ,
,  满足的等量关系.
满足的等量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 .下列条件中能使
.下列条件中能使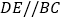 的是 ( )
的是 ( )
A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=b,则下列等式不成立的是( )
A.a+1=b+1B.1﹣a=1﹣bC.3a=3bD.2﹣3a=3b﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB;②∠DFB=
 ∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的个数是( )
∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
相关试题

