【题目】问题背景
如图![]() ,在正方形
,在正方形![]() 的内部,作
的内部,作![]() ,根据三角形全等的条件,易得
,根据三角形全等的条件,易得![]() ≌
≌![]() ≌
≌![]() ≌
≌![]() ,从而得到四边形
,从而得到四边形![]() 是正方形.
是正方形.
类比探究
如图![]() ,在正
,在正![]() 的内部,作
的内部,作![]() ,
, ![]() ,
, ![]() ,
, ![]() 两两相交于
两两相交于![]() ,
, ![]() ,
, ![]() 三点(
三点(![]() ,
, ![]() ,
, ![]() 三点不重合).
三点不重合).
(![]() )
)![]() ,
, ![]() ,
, ![]() 是否全等?如果是,请选择其中一对进行证明.
是否全等?如果是,请选择其中一对进行证明.
(![]() )
)![]() 是否为正三角形?请说明理由.
是否为正三角形?请说明理由.
(![]() )进一步探究发现,图
)进一步探究发现,图![]() 中的
中的![]() 的三边存在一定的等量关系,设
的三边存在一定的等量关系,设![]() ,
, ![]() ,
, ![]() ,请探索
,请探索![]() ,
, ![]() ,
, ![]() 满足的等量关系.
满足的等量关系.


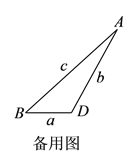
参考答案:
【答案】(1)见解析;(2)是;(3)![]()
【解析】试题分析:(1)由正三角形的性质得出∠CAB=∠ABC=∠BCA=60°,AB=BC,证出∠ABD=∠BCE,由ASA证明△ABD≌△BCE即可;
(2)由全等三角形的性质得出∠ADB=∠BEC=∠CFA,证出∠FDE=∠DEF=∠EFD,即可得出结论;
(3)作AG⊥BD于G,由正三角形的性质得出∠ADG=60°,在Rt△ADG中,DG=![]() b,AG=
b,AG=![]() b,在Rt△ABG中,由勾股定理即可得出结论.
b,在Rt△ABG中,由勾股定理即可得出结论.
试题解析:( ![]() )
)![]() ≌
≌![]() ≌
≌![]() ,理由如下:
,理由如下:
∵![]() 是正三角形,
是正三角形,
∴![]() ,
, ![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,  ,
,
∴![]() ≌
≌![]() ,
,
同理可得![]() ≌
≌![]() ,
,
∴![]() ≌
≌![]() ≌
≌![]() .
.
(![]() )
)![]() 是正三角形,理由如下.
是正三角形,理由如下.
∵![]() ≌
≌![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是正三角形.
是正三角形.
(![]() )作
)作![]() 于
于![]() ,如图所示:
,如图所示:

∵![]() 是正三角形,
是正三角形,
∴![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
在![]() 中,
中, 
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图,
 ∥
∥ ,
, ,
, ,求
,求 的度数.
的度数.小明的思路是过点
 作
作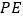 ∥
∥ ,通过平行线的性质来求
,通过平行线的性质来求 .
.
(1)按照小明的思路,求
 的度数;
的度数;(2)问题迁移:如图,
 ∥
∥ ,点
,点 在射线
在射线 上运动,记
上运动,记 ,
, ,当点
,当点 在
在 、
、 两点之间运动时,问
两点之间运动时,问 与
与 、
、 之间有何数量关系?请说明理由;
之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点
 不在
不在 、
、 两点之间运动时(点
两点之间运动时(点 与点
与点 、
、 、
、 三点不重合),请直接写出
三点不重合),请直接写出 与
与 、
、 之间的数量关系.
之间的数量关系.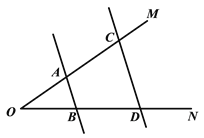
-
科目: 来源: 题型:
查看答案和解析>>【题目】正如我们小学学过的圆锥体积公式V=
 πr2h(π表示圆周率,r表示圆锥的地面半径,h表示圆锥的高)一样,许多几何量的计算都要用到π.祖冲之是世界上第一个把π计算到小数点后7位的中国古代科学家,创造了当时世界上的最高水平,差不多过了1000年,才有人把π计算得更精确.在辉煌成就的背后,我们来看看祖冲之付出了多少.现在的研究表明,仅仅就计算来讲,他至少要对9位数字反复进行130次以上的各种运算,包括开方在内.即使今天我们用纸笔来算,也绝不是一件轻松的事情,何况那时候没有现在的纸笔,数学计算不是用现在的阿拉伯数字,而是用算筹(小竹棍或小竹片)进行的,这需要怎样的细心和毅力啊!他这种严谨治学的态度,不怕复杂计算的毅力,值得我们学习.
πr2h(π表示圆周率,r表示圆锥的地面半径,h表示圆锥的高)一样,许多几何量的计算都要用到π.祖冲之是世界上第一个把π计算到小数点后7位的中国古代科学家,创造了当时世界上的最高水平,差不多过了1000年,才有人把π计算得更精确.在辉煌成就的背后,我们来看看祖冲之付出了多少.现在的研究表明,仅仅就计算来讲,他至少要对9位数字反复进行130次以上的各种运算,包括开方在内.即使今天我们用纸笔来算,也绝不是一件轻松的事情,何况那时候没有现在的纸笔,数学计算不是用现在的阿拉伯数字,而是用算筹(小竹棍或小竹片)进行的,这需要怎样的细心和毅力啊!他这种严谨治学的态度,不怕复杂计算的毅力,值得我们学习.下面我们就来通过计算解决问题:已知圆锥的侧面展开图是个半圆,若该圆锥的体积等于
 ,则这个圆锥的高等于( )
,则这个圆锥的高等于( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
 中,
中,  ,垂足为点
,垂足为点 ,
,  ,垂足为点
,垂足为点 ,
,  为
为 边的中点,连结
边的中点,连结 、
、 、
、 .
.
(
 )猜想
)猜想 的形状,并说明理由.
的形状,并说明理由.(
 )若
)若 ,
,  ,求
,求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 .下列条件中能使
.下列条件中能使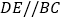 的是 ( )
的是 ( )
A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,PB是⊙O的切线,C是⊙O上的点,AC∥OP,M是直径AB上的动点,A与直线CM上的点连线距离的最小值为d,B与直线CM上的点连线距离的最小值为f.
(1)求证:PC是⊙O的切线;
(2)设OP=
 AC,求∠CPO的正弦值;
AC,求∠CPO的正弦值;(3)设AC=9,AB=15,求d+f的取值范围.

相关试题

