【题目】已知,如图,线段AD=10cm,点B,C都是线段AD上的点,且AC=7cm,BD=4cm,若E,F分别是线段AB,CD的中点,求BC与EF的长度. ![]()
参考答案:
【答案】解:由线段的和差,得 AC+BD=AC+BC+CD=AD+BC=7+4=11cm,
由AD=10cm,得10+BC=11,
解得BC=1cm;
由线段的和差,得
AB+CD=AD﹣BC=10﹣1=9cm,
由E,F分别是线段AB,CD的中点,得
AE= ![]() AB,DF=
AB,DF= ![]() CD,
CD,
由线段得和差,得
EF=AD﹣(AE+DF)=AD﹣( ![]() AB+
AB+ ![]() CD)=10﹣
CD)=10﹣ ![]() (AB+CD)=10﹣
(AB+CD)=10﹣ ![]() =
= ![]() cm
cm
【解析】根据线段的和差,可得BC的长,根据线段的和差,可得(AB+CD)的长,根据线段中点的性质,可得(AE+DF)的长,再根据线段的和差,可得EF的长.
【考点精析】本题主要考查了两点间的距离的相关知识点,需要掌握同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中变形正确的是( ) ①4x+8=0变形为x+2=0;
②x+6=5﹣2x变形为3x=﹣1;
③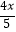 =3变形为4x=15;
=3变形为4x=15;
④4x=2变形为x=2.
A.①④
B.①②③
C.③④
D.①②④ -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:9m÷3m=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边长分别为5cm、2cm,则该等腰三角形的周长是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用“⊕”定义一种新运算:对于任意有理数a和b,规定a⊕b=ab2+2ab+a. 如:1⊕3=1×32+2×1×3+1=16.
(1)求(﹣2)⊕3的值;
(2)若(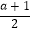 ⊕3)⊕(﹣
⊕3)⊕(﹣  )=8,求a的值.
)=8,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)(-x)5÷(-x)2=________;(2)x10÷x2÷x3÷x4=________;(3)(p-q)4÷(q-p)3=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查适合用普查的是()
A. 长江中现有鱼的种类 B. 某品牌灯泡的使用寿命 C. 夏季冷饮市场上冰淇淋的质量 D. 航天飞机的零件
相关试题

