【题目】如图,在△ABC中,三个顶点的坐标分别为A(﹣5,0),B(4,0),C(2,5),将△ABC沿x轴正方向平移2个单位长度,再沿y轴沿负方向平移1个单位长度得到△EFG.
(1)求△EFG的三个顶点坐标.
(2)求△EFG的面积.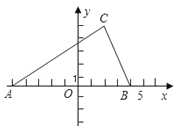
参考答案:
【答案】解:(1)如下图:E(﹣3,﹣1)、F(6,﹣1)、G(4,4);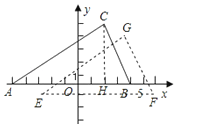
(2)如上图,过C作CH⊥AB.
∵△EFG是由△ABC沿x轴正方向平移2个单位长度,再沿y轴沿负方向平移1个单位长度得到的.
∴△EFG≌△ABC,
∴S△EFG=S△ABC ,
∵AB=|4﹣(﹣5)|=9,
CH=|5﹣0|=5,
∴S△ABC=![]() ABCH
ABCH
=![]() ×9×5
×9×5
=![]() ;
;
即S△EFG=S△ABC=![]() .
.
【解析】(1)按照题目要求,画出平移后的三角形,即可得出△EFG的三点坐标,或根据平移公式也可直接得出平移后三角形的三个顶点坐标;
(2)根据已知条件,△EFG≌△ABC,所以有S△EFG=S△ABC , 只需求出S△ABC即可,根据三角形的面积公式,易知底边AB的长度,高为点C到AB的距离,即为点C的纵坐标.
【考点精析】根据题目的已知条件,利用三角形的面积的相关知识可以得到问题的答案,需要掌握三角形的面积=1/2×底×高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6的正方形ABCD中,将正方形ABCD绕点A逆时针旋转角度α(0°<α<90°),得到正方形AEFG,EF交线段CD于点P,FE的延长线交线段BC于点H,连接AH、AP.
(1)求证:△ADP≌△AEP;
(2)①求∠HAP的度数;②判断线段HP、BH、DP的数量关系,并说明理由;
(3)连接DE、EC、CF、DF得到四边形CFDE,在旋转过程中,四边形CFDE能否为矩形?若能,求出BH的值;若不能,请说明理由.
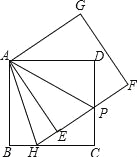
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:2(x2y+xy)﹣3(x2y﹣xy)﹣4x2y,其中x=﹣1,y=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹙3x2+2x+1﹚-﹙2x2+x-1﹚;
(2)5﹙x2-2y﹚-2﹙x2+4y﹚;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P,Q分别在∠AOB的两边OA,OB上,若点N到∠AOB的两边距离相等,且PN=NQ,则点N一定是( ).
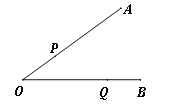
A.∠AOB的平分线与PQ的交点
B.∠OPQ与∠OQP的角平分线的交点
C.∠AOB的平分线与线段PQ的垂直平分线的交点
D.线段PQ的垂直平分线与∠OPQ的平分线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,∠B=∠C=90 ,M是BC的中点,DM平分∠ADC.
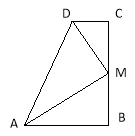
(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;
(2)线段DM与AM有怎样的位置关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,BD、CE分别是AC、AB上的高,BD与CE交于点O.BE=CD

(1)问△ABC为等腰三角形吗?为什么?
(2)问点O在∠A的平分线上吗?为什么?
相关试题

