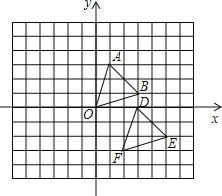
【题目】已知坐标平面内的三个点A(1,3),B(3,1),O(0,0),把△ABO向下平移3个单位再向右平2个单位后得△DEF.

(1)直接写出A、B、O三个对应点D、E、F的坐标;
(2)求△DEF的面积.
参考答案:
【答案】(1)D(3,0)、E(5,﹣2)、F(2,﹣3);(2)4
【解析】
试题分析:(1)根据点的平移规律:横坐标,右移加,左移减;纵坐标,上移加,下移减可以直接算出A、B、O三个对应点D、E、F的坐标;
(2)把△DEF放在一个矩形中,利用矩形的面积减去周围多余三角形的面积即可.
解:(1)∵点A(1,3),B(3,1),O(0,0),
∴把△ABO向下平移3个单位再向右平移2个单位后A、B、O三个对应点D(1+2,3﹣3)、E(3+2,1﹣3)、F(0+2,0﹣3),
即D(3,0)、E(5,﹣2)、F(2,﹣3);
(2)△DEF的面积:3×3﹣![]() ×1×3﹣
×1×3﹣![]() ×1×3﹣
×1×3﹣![]() ×2×2=4.
×2×2=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价.在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(xn+1)2(x2)n﹣1=( )
A.x4n
B.x4n+3
C.x4n+1
D.x4n﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.

原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线.
根据___________,SAS
易证△AFG≌___________△AEF
,得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°.点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系______________∠B+∠D=180°
时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位质数,它的个位数字与十位数字之差的经验值等于5,这样的两位质数是;
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算8a3÷(-2a)的结果是( )
A. 4a B. -4a C. 4a2 D. -4a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=
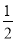 x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(6,2),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是 ,S3的值为 .
x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(6,2),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是 ,S3的值为 .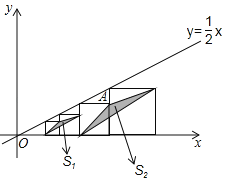
相关试题

