【题目】我市某中学为备战省运会,在校运动队的学生中进行了全能选手的选拔,并将参加选拔学生的综合成绩分成四组,绘成了如下尚不完整的统计图表.
组别 | 成绩 | 组中值 | 频数 |
第一组 | 90≤x<100 | 95 | 4 |
第二组 | 80≤x<90 | 85 | m |
第三组 | 70≤x<80 | 75 | n |
第四组 | 60≤x<70 | 65 | 21 |
根据图表信息,回答下列问题:
(1)参加活动选拔的学生共有人;表中m= , n=;
(2)若将各组的组中值视为该组的平均值,请你估算参加选拔学生的平均成绩;
(3)将第一组中的4名学生记为A、B、C、D,由于这4名学生的体育综合水平相差不大,现决定随机挑选其中两名学生代表学校参赛,试通过画树形图或列表的方法求恰好选中A和B的概率. 
参考答案:
【答案】
(1)50;10;15
(2)解: ![]() =
= ![]() =74.4
=74.4
(3)解:将第一组中的4名学生记为A、B、C、D,现随机挑选其中两名学生代表学校参赛,所有可能的结果如下表:
A | B | C | D | |
A | (B,A) | (C,A) | (D,A) | |
B | (A,B) | (C,B) | (D,B) | |
C | (A,C) | (B,C) | (D,C) | |
D | (A,D) | (B,D) | (C,D) |
由上表可知,总共有12种结果,且每种结果出现的可能性相同.恰好选中A和B的结果有2种,其概率为= ![]() =
= ![]()
【解析】解:(1)∵第一组有4人,所占百分比为8%,
∴学生总数为:4÷8%=50;
∴n=50×30%=15,
m=50﹣4﹣15﹣21=10.
所以答案是50,10,15;
【考点精析】关于本题考查的扇形统计图和列表法与树状图法,需要了解能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数
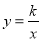 (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.(1)求△OCD的面积;
(2)当BE=
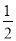 AC时,求CE的长.
AC时,求CE的长.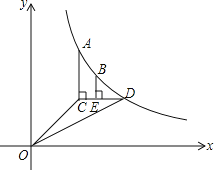
【答案】(1)
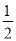 ;(2)
;(2)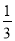 .
.【解析】试题分析:(1)根据函数
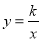 (x>0)的图象经过点A(1,2),求函数解析式,再有AC∥y轴,AC=1求出C点坐标,然后根据CD∥x轴,求D点坐标,从而可求CD长,最后利用三角形面积公式求出△OCD的面积.
(x>0)的图象经过点A(1,2),求函数解析式,再有AC∥y轴,AC=1求出C点坐标,然后根据CD∥x轴,求D点坐标,从而可求CD长,最后利用三角形面积公式求出△OCD的面积.(2)通过BE=
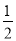 AC,求得B点坐标,进而求得CE长.
AC,求得B点坐标,进而求得CE长.试题解析:解:(1)∵函数
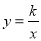 (x>0)的图象经过点A(1,2),
(x>0)的图象经过点A(1,2),∴
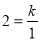 ,即k=2.
,即k=2.∵AC∥y轴,AC=1,∴点C的坐标为(1,1).
∵ CD∥x轴,点D在函数图像上,∴点D的坐标为(2,1).
∴
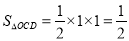 .
.(2)∵BE=
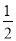 AC,∴BE=
AC,∴BE=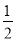 .
.∵BE⊥CD,∴点B的纵坐标是
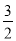 .∴点B的横坐标是
.∴点B的横坐标是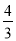 .
.∴CE=
 .
.考点:1.反比例函数综合题;3.曲线上点的坐标与方程的关系;3.三角形的面积.
【题型】解答题
【结束】
27【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:
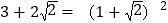 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:设
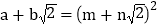 (其中
(其中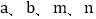 均为整数),则有
均为整数),则有 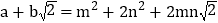 .
.∴
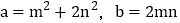 .这样小明就找到了一种把部分
.这样小明就找到了一种把部分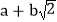 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
(1)当
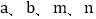 均为正整数时,若
均为正整数时,若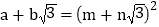 ,用含m、n的式子分别表示
,用含m、n的式子分别表示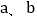 ,得
,得 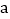 = ,
= ,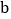 = ;
= ;(2)利用所探索的结论,找一组正整数
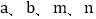 ,填空: +
,填空: + 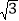 =( +
=( + 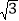 )2;
)2;(3)若
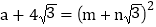 ,且
,且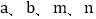 均为正整数,求
均为正整数,求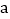 的值.
的值. -
科目: 来源: 题型:
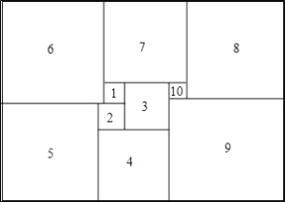
查看答案和解析>>【题目】如图所示,1925年数学家莫伦发现的世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形.若标注①、②的正方形边长分别为5和6,请你直接写出以下数据:
(1)第6个正方形的边长= ;
(2)第8个正方形的边长= ;
(3)整个长方形的面积= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年某月的月历上圈出了相邻的三个数a、b、c,并求出了它们的和为39,这三个数在月历中的排布不可能是( )
A.
 B.
B. 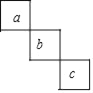 C.
C. 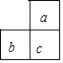 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,航空母舰始终以40千米/时的速度由西向东航行,飞机以800千米/时的速度从舰上起飞,向西航行执行任务,如果飞机在空中最多能连续飞行4个小时,那么它在起飞_____小时后就必须返航,才能安全停在舰上?

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:
 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:设
 (其中
(其中 均为整数),则有
均为整数),则有  .
.∴
 .这样小明就找到了一种把部分
.这样小明就找到了一种把部分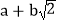 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
(1)当
 均为正整数时,若
均为正整数时,若 ,用含m、n的式子分别表示
,用含m、n的式子分别表示 ,得
,得  = ,
= , = ;
= ;(2)利用所探索的结论,找一组正整数
 ,填空: +
,填空: +  =( +
=( +  )2;
)2;(3)若
 ,且
,且 均为正整数,求
均为正整数,求 的值.
的值.【答案】(1)
 ;
; ;(2)4,2,1,1(答案不唯一);(3)
;(2)4,2,1,1(答案不唯一);(3) =7或13
=7或13【解析】分析:(1)由a+b
 =(m+n
=(m+n )2,展开比较系数可得答案;
)2,展开比较系数可得答案;(2)取m=1,n=1,可得a和b的值,可得答案;
(3)由题意得m和n的方程,解方程可得m和n,可得a值.
详解:(1)∵a+b
 =(m+n
=(m+n )2,
)2,∴a+b
 =m2+3n2+2mn
=m2+3n2+2mn ,
,∴a=m2+3n2,b=2mn.
故答案为:m2+3n2,2mn.
(2)设m=1,n=1,
∴a=m2+3n2=4,b=2mn=2.
故答案为4、2、1、1.
(3)由题意,得:
a=m2+3n2,b=2mn
∵4=2mn,且m、n为正整数,
∴m=2,n=1或者m=1,n=2,
∴a=22+3×12=7,或a=12+3×22=13.
点睛:本题主要考查二次根式的混合运算,完全平方公式,解题的关键在于熟练运算完全平方公式和二次根式的运算法则.
【题型】解答题
【结束】
28【题目】如图1,已知点A(a,0),B(0,b),且a、b满足
 ,
,□ABCD的边AD与y轴交于点E,且E为AD中点,双曲线
 经过C、D两点.
经过C、D两点.(1)若点D点纵坐标为t,则C点纵坐标为 (含t的代数式表示),k的值为 ;
(2)点P在双曲线
 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,连接FN,当T在AF上运动时,试判断∠ATH与∠AFN之间的数量关系,并说明理由。


-
科目: 来源: 题型:
查看答案和解析>>【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
相关试题

