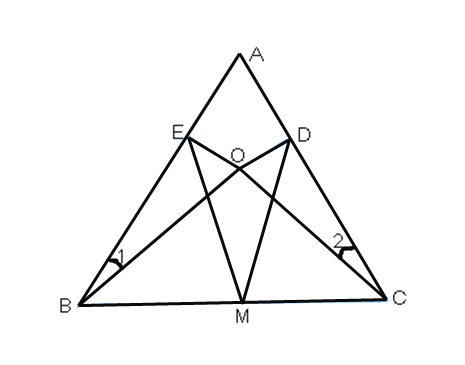
【题目】(1)已知:如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,M是BC的中点.求证:MD=ME.
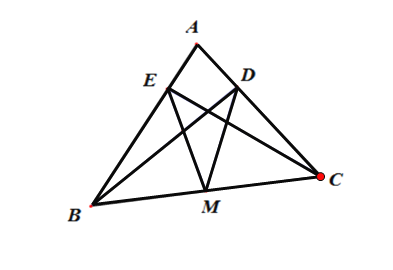
(2)已知:如图,O是△ABC内任意一点,且满足∠1=∠2,OD⊥AC于D, OE⊥AB于E,M是BC的中点。仿照第⑴问的思路,结合三角形中位线定理,平行四边形的性质与判定,求证:MD=ME.
参考答案:
【答案】(1)见详解;(2)见详解.
【解析】
(1)由BD⊥AC于D,CE⊥AB于E,则△BCD,△BCE是直角三角形,由点M是BC中点,即可得到EM=DM=![]() ;
;
(2)分别取BO中点F、CO中点G,连接EF、FM、DG、GM,由直角三角形斜边上的中线等于斜边的一半,得到EF=BF=OF=![]() OB,DG=OG=CG=
OB,DG=OG=CG=![]() OC,然后根据∠1=∠2,得到∠EFO=∠DGO;由三角形中位线定理,得到四边形OFMG是平行四边形,则∠OFM=∠OGM,从而得到∠EFM=∠DGM,利用SAS证明△EFM≌△MGD,即可得到结论成立.
OC,然后根据∠1=∠2,得到∠EFO=∠DGO;由三角形中位线定理,得到四边形OFMG是平行四边形,则∠OFM=∠OGM,从而得到∠EFM=∠DGM,利用SAS证明△EFM≌△MGD,即可得到结论成立.
证明:(1)如图,
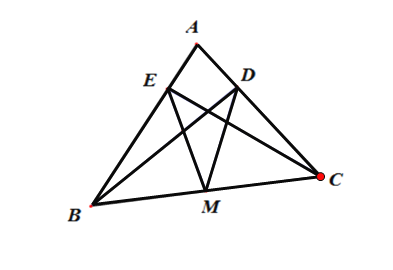
∵BD⊥AC于D,CE⊥AB于E,
∴△BCD,△BCE是直角三角形,
∵点M是BC中点,
∴ME,MD分别是直角三角形△BCE和△BCD的中线,
∴EM=DM=![]() ;
;
(2)如图,分别取BO中点F、CO中点G,连接EF、FM、DG、GM,
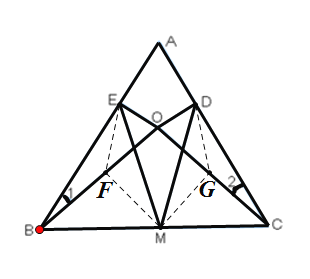
∵OD⊥AC于D,OE⊥AB于E,
∴△OBE、△OCD是直角三角形,
∵点F为OB中点,点G为OC中点,
∴EF=BF=OF=![]() OB,DG=OG=CG=
OB,DG=OG=CG=![]() OC,
OC,
∴∠1=∠BEF,∠2=∠CDG,
∴∠EFO=2∠1,∠DGO=2∠2,
∵∠1=∠2,
∴∠EFO=∠DGO,
∵点M是BC的中点,
∴FM和GM都是△OBC的中位线,
∴FM=![]() OC=OG=DG,GM=
OC=OG=DG,GM=![]() OB=OF=EF,
OB=OF=EF,
∴四边形OFMG是平行四边形,
∴∠OFM=∠OGM,
∴∠EFO+∠OFM=∠DGO+∠OGM,
即∠EFM=∠DGM,
∵FM=DG,EF=MG,
∴△EFM≌△MGD(SAS),
∴EM=MD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把长方形ABCD沿对角线BD折叠,重合部分为△EBD.
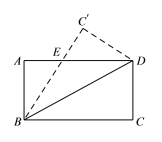
(1)求证:△EBD为等腰三角形;
(2)若AB=2,BC=8,求AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+4(k≠0)与x轴、y轴分别交于点B,A,直线y=-2x+1与y轴交于点C,与直线y=kx+4交于点D,△ACD的面积是
 .
.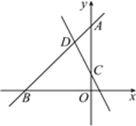
(1)求直线AB的表达式;
(2)设点E在直线AB上,当△ACE是直角三角形时,求出点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“欢乐跑中国重庆站”比赛前夕,小刚和小强相约晨练跑步.小刚比小强早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行跑步比赛.比赛时小刚的速度始终是180米/分,小强的速度是220米/分.比赛开始10分钟后,因雾霾严重,小强突感身体不适,于是他按原路以出门时的速度返回,直到他们再次相遇.如图所示是小刚、小强之间的距离y(千米)与小刚跑步所用时间x(分钟)之间的函数图象.问小刚从家出发到他们再次相遇时,一共用了__分钟.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣2,﹣1,0,1,2,3,4这7个数中任选一个数作为a的值,则使得关于x的分式方程
 有整数解,且关于x的一次函数y=(a+1)x+a﹣4的图象不经过第二象限的概率是 .
有整数解,且关于x的一次函数y=(a+1)x+a﹣4的图象不经过第二象限的概率是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC中,∠ACB=90°,CD⊥AB,M是AB的中点,若CM=2CD,则下列结论中错误的是( )
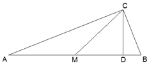
A.CB=
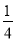 ABB.CD=
ABB.CD= MDC.∠BCM=75°D.∠ACM=15°
MDC.∠BCM=75°D.∠ACM=15° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图Rt△ABC中∠ACB=90°,将其折叠使点A落在边BC的点A′处,折痕为CD,若∠A′DB=20°,则∠B=( )
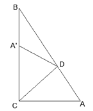
A.45°B.35°C.30°D.40°
相关试题

