【题目】如图,直线y=kx+4(k≠0)与x轴、y轴分别交于点B,A,直线y=-2x+1与y轴交于点C,与直线y=kx+4交于点D,△ACD的面积是![]() .
.
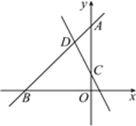
(1)求直线AB的表达式;
(2)设点E在直线AB上,当△ACE是直角三角形时,求出点E的坐标.
参考答案:
【答案】(1)y=x+4;(2)点E的坐标为(![]() 3,1)或(
3,1)或(![]()
![]() ,
,![]() ).
).
【解析】
(1)将x=0分别代入两个一次函数表达式中求出点A、C的坐标,进而即可得出AC的长度,再根据三角形的面积公式结合△ACD的面积即可求出点D的横坐标,利用一次函数图象上点的坐标特即可求出点D的坐标,由点D的坐标利用待定系数法即可求出直线AB的表达式;
(2)由直线AB的表达式即可得出△ACE为等腰直角三角形,分∠ACE=90°和∠AEC=90°两种情况考虑,根据点A、C的坐标利用等腰直角三角形的性质即可得出点E的坐标,此题得解.
解:(1)当x=0时,y=kx+4=4,y=-2x+1=1,
∴A(0,4),C(0,1),
∴AC=3.
∵S△ACD=![]() ,
,
∴![]() ,
,
∵点D在第二象限,
点D的横坐标为![]() .
.
当x=![]() 时,y=
时,y=![]() 2x+1=3,
2x+1=3,
∴D(![]() 1,3).
1,3).
将D(![]() 1,3)代入y=kx+4,
1,3)代入y=kx+4,
![]() k+4=3,解得:k=1.
k+4=3,解得:k=1.
∴直线AB的表达式为:y=x+4.
(2)∵直线AB的表达式为y=x+4,
∴△ACE为等腰直角三角形.
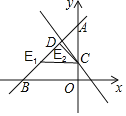
当∠ACE=90°时,∵A(0,4),C(0,1),AC=3,
∴E1(![]() 3,1);
3,1);
当∠AEC=90°时,∵A(0,4),C(0,1),AC=3,
∴E2(![]()
![]() ,
,![]() ).
).
综上所述:当△ACE是直角三角形时,点E的坐标为(![]() 3,1)或(
3,1)或(![]()
![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x<100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
分数段
频数
频率
60≤x<70
18
0.36
70≤x<80
17
c
80≤x<90
a
0.24
90≤x<100
b
0.06
合计
1

根据以上信息解答下列问题:
(1)统计表中c的值为________;样本成绩的中位数落在分数段________中;
(2)补全频数直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评的作品数量是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把长方形ABCD沿对角线BD折叠,重合部分为△EBD.
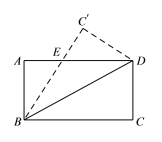
(1)求证:△EBD为等腰三角形;
(2)若AB=2,BC=8,求AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“欢乐跑中国重庆站”比赛前夕,小刚和小强相约晨练跑步.小刚比小强早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行跑步比赛.比赛时小刚的速度始终是180米/分,小强的速度是220米/分.比赛开始10分钟后,因雾霾严重,小强突感身体不适,于是他按原路以出门时的速度返回,直到他们再次相遇.如图所示是小刚、小强之间的距离y(千米)与小刚跑步所用时间x(分钟)之间的函数图象.问小刚从家出发到他们再次相遇时,一共用了__分钟.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知:如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,M是BC的中点.求证:MD=ME.
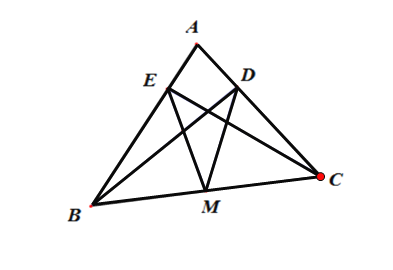
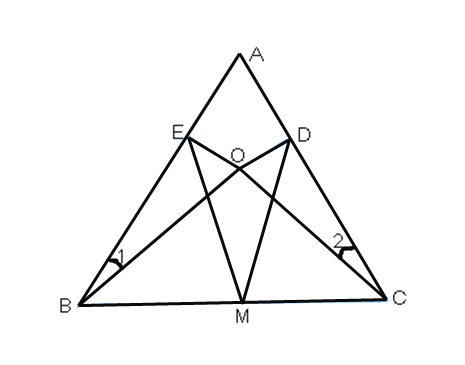
(2)已知:如图,O是△ABC内任意一点,且满足∠1=∠2,OD⊥AC于D, OE⊥AB于E,M是BC的中点。仿照第⑴问的思路,结合三角形中位线定理,平行四边形的性质与判定,求证:MD=ME.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣2,﹣1,0,1,2,3,4这7个数中任选一个数作为a的值,则使得关于x的分式方程
 有整数解,且关于x的一次函数y=(a+1)x+a﹣4的图象不经过第二象限的概率是 .
有整数解,且关于x的一次函数y=(a+1)x+a﹣4的图象不经过第二象限的概率是 .
相关试题

