【题目】如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D. 
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=2 ![]() ,求PD的长.
,求PD的长.
参考答案:
【答案】
(1)证明:∵∠ABC=∠APC,∠BAC=∠BPC,∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC是等边三角形
(2)解:∵△ABC是等边三角形,AB=2 ![]() ,
,
∴AC=BC=AB=2 ![]() ,∠ACB=60°.
,∠ACB=60°.
在Rt△PAC中,∠PAC=90°,∠APC=60°,AC=2 ![]() ,
,
∴AP= ![]() =2.
=2.
在Rt△DAC中,∠DAC=90°,AC=2 ![]() ,∠ACD=60°,
,∠ACD=60°,
∴AD=ACtan∠ACD=6.
∴PD=AD﹣AP=6﹣2=4
【解析】(1)由圆周角定理可知∠ABC=∠BAC=60°,从而可证得△ABC是等边三角形;(2)由△ABC是等边三角形可得出“AC=BC=AB=2 ![]() ,∠ACB=60°”,在直角三角形PAC和DAC通过特殊角的正、余切值即可求出线段AP、AD的长度,二者作差即可得出结论.
,∠ACB=60°”,在直角三角形PAC和DAC通过特殊角的正、余切值即可求出线段AP、AD的长度,二者作差即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )
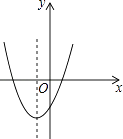
A.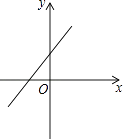
B.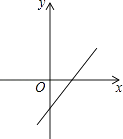
C.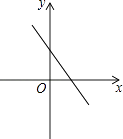
D.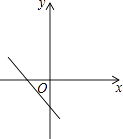
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=
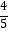 ,反比例函数y=
,反比例函数y= 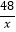 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于 .
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于 . 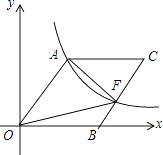
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有客房50间,当每间客房每天的定价为220元时,客房会全部住满;当每间客房每天的定价增加10元时,就会有一间客房空闲,设每间客房每天的定价增加x元时,客房入住数为y间.
(1)求y与x的函数关系式(不要求写出x的取值范围);
(2)如果每间客房入住后每天的各种支出为40元,不考虑其他因素,则该宾馆每间客房每天的定价为多少时利润最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax2+bx(a≠0)表示.已知抛物线上B,C两点到地面的距离均为
 m,到墙边OA的距离分别为
m,到墙边OA的距离分别为  m,
m,  m.
m. 
(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10m,则最多可以连续绘制几个这样的拋物线型图案? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.

相关试题

