【题目】课本中有一个例题: 有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2 .
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题: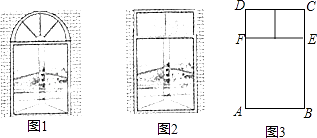
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
参考答案:
【答案】
(1)解:由已知可得:AD= ![]() ,
,
则S=1× ![]() m2
m2
(2)解:设AB=xm,则AD=3﹣ ![]() m,
m,
∵ ![]() ,
,
∴ ![]() ,
,
设窗户面积为S,由已知得:
![]() ,
,
当x= ![]() m时,且x=
m时,且x= ![]() m在
m在 ![]() 的范围内,
的范围内, ![]() ,
,
∴与课本中的例题比较,现在窗户透光面积的最大值变大
【解析】(1)根据矩形和正方形的周长进行解答即可;(2)设AB为xcm,利用二次函数的最值解答即可.
-
科目: 来源: 题型:
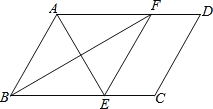
查看答案和解析>>【题目】如图,在□ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.
(1)求证:四边形ABEF是菱形;
(2)若AB=10,BF=16,AD=15, 则□ABCD 的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.
如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点.
知识运用:
(1)如图1,表示0的点D到点A的距离是1,到点B的距离是2,那么点D 【A,B】的好点;(请在横线上填是或不是)
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2.数 所对应的点是【M,N】的好点(写出所有可能的情况);
拓展提升:
(3)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当经过几秒时,P、A和B中恰有一个点为其余两点的好点?(写出所有情况)
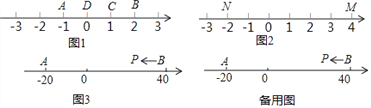
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D.
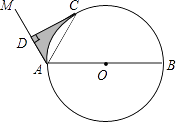
(1)求证:CD是⊙O的切线;
(2)若∠ACD=30°,AD=4,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某村计划对总长为1800m的道路进行改造,安排甲、乙两个工程队完成.已知甲队每天能完成的道路长度是乙队每天能完成的2倍,并且在独立完成长为400m的道路时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成道路的长度分别是多少m?
(2)若村委每天需付给甲队的道路改造费用为0.4万元,乙队为0.25万元,要使这次的道路改造费用不超过8万元,至少应安排甲队工作多少天?
-
科目: 来源: 题型:
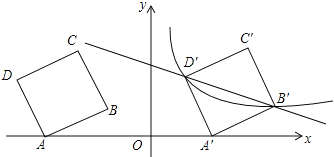
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(
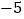 ,0)、D(
,0)、D( ,3),点B、C在第二象限内.
,3),点B、C在第二象限内.(1)点B的坐标 ;
(2)将正方形ABCD以每秒2个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图像上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在y轴上的点P和反比例函数图像上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(9)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
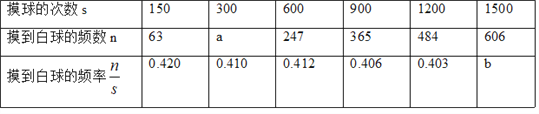
(1)按表格数据格式,表中的a= ;b= ;
(2)请估计:当次数s很大时,摸到白球的频率将会接近 ;
(3)请推算:摸到红球的概率是 (精确到0.1);
(4)试估算:口袋中红球有多少只?
相关试题

