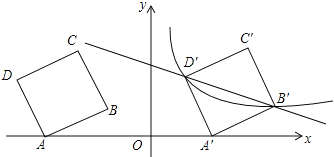
【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(![]() ,0)、D(
,0)、D(![]() ,3),点B、C在第二象限内.
,3),点B、C在第二象限内.
(1)点B的坐标 ;
(2)将正方形ABCD以每秒2个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图像上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在y轴上的点P和反比例函数图像上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)B(-2,1);(2)t=4,反比例函数解析式为![]() ;
;
(3)当B′D′为对角线时,![]() ,
,![]() ;当B′D′为边时,
;当B′D′为边时,![]() ,
,![]() 或
或![]() ,
,![]()
【解析】分析:(1)过点D作DE⊥x轴于点E,过点B作BF⊥x轴于点F,由正方形的性质结合同角的余角相等即可证出△ADE≌△BAF,从而得出DE=AF,AE=BF,再结合点A、D的坐标即可求出点B的坐标;
(2)设反比例函数为y=![]() ,根据平行的性质找出点B′、D′的坐标,再结合反比例函数图象上点的坐标特征即可得出关于k、t的二元一次方程组,解方程组解得出结论;
,根据平行的性质找出点B′、D′的坐标,再结合反比例函数图象上点的坐标特征即可得出关于k、t的二元一次方程组,解方程组解得出结论;
(3)假设存在,设点P的坐标为(m,0),点Q的坐标为(n,![]() ).分B′D′为对角线或为边考虑,根据平行四边形的性质找出关于m、n的方程组,解方程组即可得出结论.
).分B′D′为对角线或为边考虑,根据平行四边形的性质找出关于m、n的方程组,解方程组即可得出结论.
详解:(1)过点D作DE⊥x轴于点E,过点B作BF⊥x轴于点F,如图1所示.

∵四边形ABCD为正方形,
∴AD=AB,∠BAD=90°,
∵∠EAD+∠ADE=90°,∠EAD+∠BAF=90°,
∴∠ADE=∠BAF.
在△ADE和△BAF中,
 ,
,
∴△ADE≌△BAF(AAS),
∴DE=AF,AE=BF.
∵点A(-6,0),D(-7,3),
∴DE=3,AE=1,
∴点B的坐标为(-6+3,0+1),即(-3,1).
故答案为:(-3,1).
(2)设反比例函数为y=![]() ,
,
由题意得:点B′坐标为(-3+t,1),点D′坐标为(-7+t,3),
∵点B′和D′在该比例函数图象上,
∴k=(-3+t)×1=(-7+t)×3,
解得:t=9,k=6,
∴反比例函数解析式为y=![]() .
.
(3)假设存在,设点P的坐标为(m,0),点Q的坐标为(n,![]() ).
).
以P、Q、B′、D′四个点为顶点的四边形是平行四边形分两种情况:
当B′D′为对角线时,![]() ,
,![]()
当B′D′为边时, ![]() ,
,![]() 或
或![]() ,
,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D.
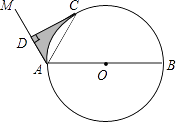
(1)求证:CD是⊙O的切线;
(2)若∠ACD=30°,AD=4,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】课本中有一个例题: 有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2 .
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题: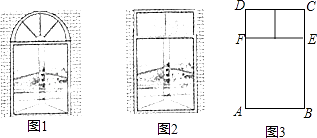
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】某村计划对总长为1800m的道路进行改造,安排甲、乙两个工程队完成.已知甲队每天能完成的道路长度是乙队每天能完成的2倍,并且在独立完成长为400m的道路时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成道路的长度分别是多少m?
(2)若村委每天需付给甲队的道路改造费用为0.4万元,乙队为0.25万元,要使这次的道路改造费用不超过8万元,至少应安排甲队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(9)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
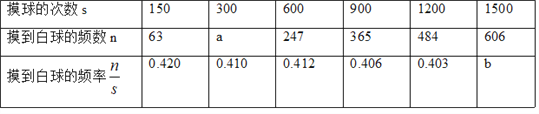
(1)按表格数据格式,表中的a= ;b= ;
(2)请估计:当次数s很大时,摸到白球的频率将会接近 ;
(3)请推算:摸到红球的概率是 (精确到0.1);
(4)试估算:口袋中红球有多少只?
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.
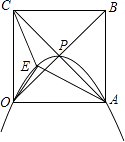
(1)建立适当的平面直角坐标系,
①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)求△OAE与△OCE面积之和的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】自行车厂某周计划生产2100辆电动车,平均每天生产电动车300辆.由于各种原因,实际每天的生产量与计划每天的生产量相比有出入,下表是该周的实际生产情况(超产记为正、减产记为负,单位:辆):
星期
一
二
三
四
五
六
日
减增







(1)该厂星期一生产电动车________辆;
(2)生产量最多的一天比生产量最少的一天多生产电动车________辆;
(3)该厂实行记件工资制,每生产一辆车可得60元,那么该厂工人这一周的工资总额是多少元?
相关试题

