【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 2 | 5 | 1 | 5 | 4 | 7 | 4 | 3 | 3 | 6 |
根据以上数据,解答下列问题:
(I)直接填空:第10次摸棋子摸到黑棋子的频率为 ;
(Ⅱ)试估算袋中的白棋子数量.
参考答案:
【答案】(1)0.9(2)白棋子的数量约为15枚
【解析】
(I)用第10次黑棋数除以第10次摸出的棋子总数可得答案;
(Ⅱ)先求出这10次摸出黑棋的总数占摸出的棋子总数的频率,再设白棋子有x枚,根据黑棋子数的频率列出关于x的方程,解之求得x的值可得答案.
解:(I)第10次摸棋子摸到黑棋子的频率为6÷10=0.6,
故答案为:0.6;
(Ⅱ)根据表格中数据知,摸到黑棋子的频率为![]() =0.4,
=0.4,
设白棋子有x枚,
由题意,得:![]() =0.4,
=0.4,
解得:x=15,
经检验:x=15是原分式方程的解,
答:白棋子的数量约为15枚.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解食品安全状况,质监部门抽查了甲、乙、丙、丁四个品牌饮料的质量,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,完成下列问题:
(1)这次抽查了四个品牌的饮料共 瓶;
(2)请你在答题卡上补全两幅统计图;
(3)若四个品牌饮料的平均合格率是95%,四个品牌饮料月销售量约20万瓶,请你估计这四个品牌的不合格饮料有多少瓶?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点E、F分别在AB、BC上,△DEF为等腰直角三角形,∠DEF=90°,AD+CD=10,AE=2,求AD的长.
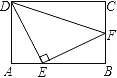
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+1(a<0)的图象过点(1,0)和(x1 , 0),且﹣2<x1<﹣1,下列5个判断中:①b<0;②b﹣a<0;③a>b﹣1;④a<﹣
 ;⑤2a<b+
;⑤2a<b+  ,正确的是( )
,正确的是( )
A.①③
B.①②③
C.①②③⑤
D.①③④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在x轴的上方,直角∠BOA绕原点O顺时针方向旋转,若∠BOA的两边分别与函数y=﹣
 、y=
、y=  的图象交于B、A两点,则tanA= .
的图象交于B、A两点,则tanA= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图四边形ABCD中,AD=DC,∠DAB=∠ACB=90°,过点D作DF⊥AC,垂足为F.DF与AB相交于E.设AB=15,BC=9,P是射线DF上的动点.当△BCP的周长最小时,DP的长为 .
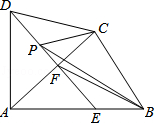
-
科目: 来源: 题型:
查看答案和解析>>【题目】一块长方体木块的各棱长如图所示,一只蜘蛛在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处,蜘蛛急于捉住苍蝇,沿着长方体的表面向上爬.
(1)如果D是棱的中点,蜘蛛沿“AD→DB”路线爬行,它从A点爬到B点所走的路程为多少?
(2)你认为“AD→DB”是最短路线吗?如果你认为不是,请计算出最短的路程.

相关试题

