【题目】如图1,抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求a的值和直线AB的函数表达式;
(2)设△PMN的周长为C1 , △AEN的周长为C2 , 若 ![]() =
= ![]() ,求m的值;
,求m的值;
(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接E′A、E′B,求E′A+ ![]() E′B的最小值.
E′B的最小值.
参考答案:
【答案】
(1)
解:令y=0,则ax2+(a+3)x+3=0,
∴(x+1)(ax+3)=0,
∴x=﹣1或﹣ ![]() ,
,
∵抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),
∴﹣ ![]() =4,
=4,
∴a=﹣ ![]() .
.
∵A(4,0),B(0,3),
设直线AB解析式为y=kx+b,则 ![]() ,
,
解得 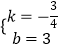 ,
,
∴直线AB解析式为y=﹣ ![]() x+3
x+3
(2)
解:如图1中,

∵PM⊥AB,PE⊥OA,
∴∠PMN=∠AEN,∵∠PNM=∠ANE,
∴△PNM∽△ANE,
∴ ![]() =
= ![]() ,
,
∵NE∥OB,
∴ ![]() =
= ![]() ,
,
∴AN= ![]() (4﹣m),
(4﹣m),
∵抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+3,
x+3,
∴PN=﹣ ![]() m2+
m2+ ![]() m+3﹣(﹣
m+3﹣(﹣ ![]() m+3)=﹣
m+3)=﹣ ![]() m2+3m,
m2+3m,
∴  =
= ![]() ,
,
解得m=2.
(3)
解:如图2中,在y轴上 取一点M使得OM= ![]() ,
,

∵OE′=2,OMOB= ![]() ×3=4,
×3=4,
∴OE′2=OMOB,
∴ ![]() =
= ![]() ,∵∠BOE′=∠MOE′,
,∵∠BOE′=∠MOE′,
∴△MOE′∽△E′OB,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ME′= ![]() BE′,
BE′,
∴AE′+ ![]() BE′=AE′+E′M=AM′,
BE′=AE′+E′M=AM′,
此时AE′+ ![]() BE′最小,最小值=AM=
BE′最小,最小值=AM= ![]() =
= ![]()
![]()
【解析】(1)令y=0,求出抛物线与x轴交点,列出方程即可求出a,根据待定系数法可以确定直线AB解析式.(2)由△PNM∽△ANE,推出 ![]() =
= ![]() ,列出方程即可解决问题.(3)在y轴上 取一点M使得OM=
,列出方程即可解决问题.(3)在y轴上 取一点M使得OM= ![]() ,构造相似三角形,可以证明AM就是E′A+
,构造相似三角形,可以证明AM就是E′A+ ![]() E′B的最小值.本题考查相似三角形的判定和性质、待定系数法、最小值问题等知识,解题的关键是构造相似三角形,找到线段AM就是E′A+
E′B的最小值.本题考查相似三角形的判定和性质、待定系数法、最小值问题等知识,解题的关键是构造相似三角形,找到线段AM就是E′A+ ![]() E′B的最小值,属于中考压轴题.
E′B的最小值,属于中考压轴题.
【考点精析】利用二次函数的最值和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,OABC的边OC在x轴的正半轴上,OC=5,反比例函数y=
 (x>0)的图象经过点A(1,4).
(x>0)的图象经过点A(1,4).
(1)求反比例函数的关系式和点B的坐标;
(2)如图2,过BC的中点D作DP∥x轴交反比例函数图象于点P,连接AP、OP.
①求△AOP的面积;
②在OABC的边上是否存在点M,使得△POM是以PO为斜边的直角三角形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了图形的旋转知识后,数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究.

(一)尝试探究
如图1,在四边形ABCD中,AB=AD,∠BAD=60°,∠ABC=∠ADC=90°,点E、F分别在线段BC、CD上,∠EAF=30°,连接EF.
(1)如图2,将△ABE绕点A逆时针旋转60°后得到△A′B′E′(A′B′与AD重合),请直接写出∠E′AF=度,线段BE、EF、FD之间的数量关系为 .
(2)如图3,当点E、F分别在线段BC、CD的延长线上时,其他条件不变,请探究线段BE、EF、FD之间的数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线OB是一次函数y=2x的图象,点A的坐标是(0,2),点C在直线OB上且△ACO为等腰三角形,求C点坐标.
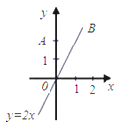
-
科目: 来源: 题型:
查看答案和解析>>【题目】穿越青海境内的兰新高铁极大地改善了沿线人民的经济文化生活,该铁路沿线甲,乙两城市相距480km,乘坐高铁列车比乘坐普通快车能提前4h到达,已知高铁列车的平均行驶速度比普通列车快160km/h,设普通列车的平均行驶速度为xkm/h,依题意,下面所列方程正确的是( )
A. ﹣
﹣  =4
=4
B. =4
=4
C.
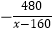 =4
=4
D.
 =4
=4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S9的值为( )

A.( )6
)6
B.( )7
)7
C.( )6
)6
D.( )7
)7
相关试题

