【题目】如图,正方形ABCD的边长为2,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S9的值为( ) 
A.( ![]() )6
)6
B.( ![]() )7
)7
C.( ![]() )6
)6
D.( ![]() )7
)7
参考答案:
【答案】A
【解析】解:在图中标上字母E,如图所示. 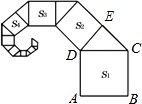
∵正方形ABCD的边长为2,△CDE为等腰直角三角形,
∴DE2+CE2=CD2 , DE=CE,
∴S2+S2=S1 .
观察,发现规律:S1=22=4,S2= ![]() S1=2,S3=
S1=2,S3= ![]() S2=1,S4=
S2=1,S4= ![]() S3=
S3= ![]() ,…,
,…,
∴Sn=( ![]() )n﹣3 .
)n﹣3 .
当n=9时,S9=( ![]() )9﹣3=(
)9﹣3=( ![]() )6 ,
)6 ,
故选:A.
根据等腰直角三角形的性质可得出S2+S2=S1 , 写出部分Sn的值,根据数的变化找出变化规律“Sn=( ![]() )n﹣3”,依此规律即可得出结论.本题考查了等腰直角三角形的性质、勾股定理以及规律型中数的变化规律,解题的关键是找出规律“Sn=(
)n﹣3”,依此规律即可得出结论.本题考查了等腰直角三角形的性质、勾股定理以及规律型中数的变化规律,解题的关键是找出规律“Sn=( ![]() )n﹣3”.本题属于中档题,难度不大,解决该题型题目时,写出部分Sn的值,根据数值的变化找出变化规律是关键.
)n﹣3”.本题属于中档题,难度不大,解决该题型题目时,写出部分Sn的值,根据数值的变化找出变化规律是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.

(1)求a的值和直线AB的函数表达式;
(2)设△PMN的周长为C1 , △AEN的周长为C2 , 若 =
=  ,求m的值;
,求m的值;
(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接E′A、E′B,求E′A+ E′B的最小值.
E′B的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】穿越青海境内的兰新高铁极大地改善了沿线人民的经济文化生活,该铁路沿线甲,乙两城市相距480km,乘坐高铁列车比乘坐普通快车能提前4h到达,已知高铁列车的平均行驶速度比普通列车快160km/h,设普通列车的平均行驶速度为xkm/h,依题意,下面所列方程正确的是( )
A. ﹣
﹣  =4
=4
B. =4
=4
C.
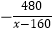 =4
=4
D.
 =4
=4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣32+6cos45°﹣
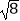 +|
+|  ﹣3|
﹣3| -
科目: 来源: 题型:
查看答案和解析>>【题目】甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为(
 ,
, ),请解决以下问题:
),请解决以下问题:(1)甲比乙晚出发几小时?
(2)分别求出甲、乙二人的速度;
(3)丙骑摩托车与乙同时出发,从N地沿同一条公路匀速前往M地,若丙经过
 h与乙相遇.
h与乙相遇.①设丙与M地的距离为S(km),行驶的时间为t(h),求S与t之间的函数关系式(不用写自变量的取值范围)
②丙与乙相遇后再用多少时间与甲相遇.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,点E,F在对角线AC上,且AE=CF.求证:

(1)DE=BF;
(2)四边形DEBF是平行四边形.
相关试题

