搜索
【题目】定义一种对正整数n的“C运算”：①当n为奇数时，结果为3n＋1；②当n为偶数时，结果为
（其中k是使为奇数的正整数），并且运算重复进行．例如，n＝66时，其“C运算”如下
若n＝26，则第2019次“C运算”的结果是
A. 40 B. 5 C. 4 D. 1
参考答案：
【答案】D
【解析】
根据定义的新规则先找出规律，再根据规律得到结果.
①当n为奇数时，结果为3n＋1；②当n为偶数时，结果为
（其中k是使为奇数的正整数），并且运算重复进行.
若n＝26，第一次n=13
第二次n=40
第三次n=5
第四次n=16
第五次n=1
第六次n=4
第七次n=1
以此可以看出，后面的结果将以1,4为规律，欧数次是4，奇数次是1,2019为奇数，所以结果为1.
故选D
-
科目： 来源： 题型：
查看答案和解析>>【题目】某“数学兴趣小组”根据学习函数的经验，对函数y=
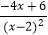的图象和性质进行了探究，探究过程如下，请补充完整：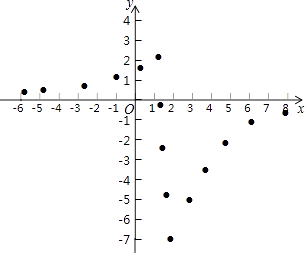
（1）该函数的自变量x的取值范围是；
（2）同学们先找到y与x的几组对应值，然后在下图的平面直角坐标系xOy中，描出各对对应值为坐标的点．请你根据描出的点，画出该函数的图象；
（3）结合画出的函数图象，写出该函数的一条性质： ． -
科目： 来源： 题型：
查看答案和解析>>【题目】某厂计划生产A、B两种产品共50件．已知A产品每件可获利润1200元，B产品每件可获利润700元，设生产两种产品的获利总额为y（元），生产A产品x（件）．
(1)写出y与x之间的函数关系式；
(2)若生产A、B两种产品的件数均不少于10件，求总利润的最大值．
-
科目： 来源： 题型：
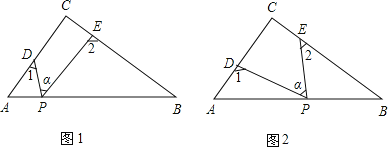
查看答案和解析>>【题目】Rt△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点.令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α.
（1）若点P在线段AB上，如图（1）所示，且∠α=50°，则∠1+∠2= °；
（2）若点P在边AB上运动，如图（2）所示，则∠α、∠1、∠2之间的关系为： ；
（3）若点P运动到边AB的延长线上，如图（3）所示，则∠α、∠1、∠2之间有何关系？猜想并说明理由.
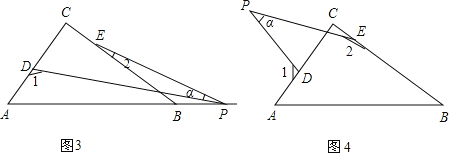
（4）若点P运动到△ABC形外，如图（4）所示，则∠α、∠1、∠2之间的关系为： .
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，PA切⊙O于点A，PO交⊙O于点C，连接BC，∠P=∠B．
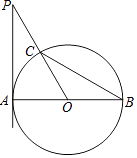
（1）求∠P的度数；
（2）连接PB，若⊙O的半径为a，写出求△PBC面积的思路．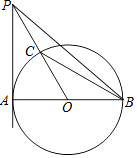
-
科目： 来源： 题型：
查看答案和解析>>【题目】填空，完成下列说理过程
如图，∠AOB＝90°，∠COD＝90°，OA平分∠DOE，若∠BOC＝20°，求∠COE的度数
解：因为∠AOB＝90°．
所以∠BOC+∠AOC＝90°
因为∠COD＝90°
所以∠AOD+∠AOC＝90°．
所以∠BOC＝∠AOD． （ ）
因为∠BOC＝20°．
所以∠AOD＝20°．
因为OA平分∠DOE
所以∠ ＝2∠AOD＝ °． （ ）
所以∠COE＝∠COD﹣∠DOE＝ °
-
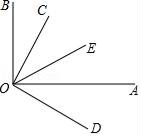
科目： 来源： 题型：
查看答案和解析>>【题目】2018年9月17日世界人工智能大会在上海召开，人工智能的变革力在教育、制造等领域加速落地. 在某市举办的一次中学生机器人足球赛中，有四个代表队进入决赛，决赛中，每个队分别与其它三个队进行主客场比赛各一场（即每个队要进行6场比赛），以下是积分表的一部分.
排名
代表队
场次
（场）
胜
（场）
平
（场）
负
（场）
净胜球
（个）
进球
（个）
失球
（个）
积分
（分）
1
A
6
1
6
12
6
22
2
B
6
3
2
1
0
6
6
19
3
C
6
3
1
2
2
9
7
17
4
D
6
0
0
6
m
5
13
0
（说明：积分＝胜场积分＋平场积分＋负场积分）
（1）D代表队的净胜球数m= ；
（2）本次决赛中，胜一场积 分，平一场积 分，负一场积 分；
（3）此次竞赛的奖金分配方案为：进入决赛的每支代表队都可以获得参赛奖金6000元；另外，在决赛期间，每胜一场可以再获得奖金2000元，每平一场再获得奖金1000元.
请根据表格提供的信息，求出冠军A队一共能获得多少奖金.
相关试题
