【题目】判断正误,并说明理由(1)给定一组数据,那么这组数据的众数有可能不唯一________;理由________(2)给定一组数据,那么这组数据的平均数一定是这组数据中的一个数________;
理由________(3)n个数的中位数一定是这n个数中的某一个________;理由________(4)求9个数据(x1、x2、……、x9 , 其平均数为m)的标准差S, 计算公式为:![]() ________;理由________
________;理由________
参考答案:
【答案】(1)正确; (2)错误;(3)错误;(4)正确.
【解析】
试题分析:(1)因为众数是一组数据中出现次数最多的数,那么众数有可能不唯一,(2)利用平均数的计算公式计算,一组数据的平均数,有可能是这组数据中的数据也有可能不是这组数据中的数据,(3) 中位数是指将一组数据按顺序排列后,最中间的数或最中间的两个数的平均数,所以中位不一定是这组数据中的某一个数据,(4)根据方差是一组数据每个数据与这组数据平均数差的平方的平均数,标准差是方差的算术平方根可以进行判定.
试题解析:(1)正确,众数是一组数据中出现次数最多的数据,注意众数可以不止一个
(2)错误,不一定,答案不唯一,如:4,6,7这组数据的平均数是![]() ,
,
(3)错误,不一定,当数据的个数是双数时,中位数是中间两个数的平均数,答案不唯一,如:2,3,4,5这组数据的中位数是![]() ,
,
(4)正确,标准差=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
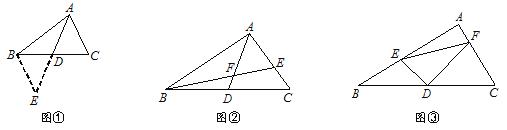
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
【灵活运用】
如图③,在△ABC中, ∠A=90°,D为BC中点, DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了从甲、乙两名射击运动员中选拔一名参加比赛,对这两名运动员进行测试,他们10次射击命中的环数如下:
甲
7
9
8
6
10
7
9
8
6
10
乙
7
8
9
8
8
6
8
9
7
10
根据测试成绩,你认为选择哪一名运动员参赛更好?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在对全市初中生的体质健康测试中,青少年体质研究中心随机抽取的10名女生的立定跳远的成绩(单位:厘米)如下:123,191,216,191,159,206,191,210,186,227.
(1)通过计算,样本数据(10名女生的成绩)的平均数是190厘米,中位数是多少厘米?众数是多少厘米?
(2)本市一初中女生的成绩是194厘米,你认为她的成绩如何?说明理由;
(3)研究中心分别确定了一个标准成绩,等于或大于这个成绩的女学生该项素质分别被评定为“合格”、“优秀”等级,其中合格的标准为大多数女生能达到,“优秀”的标准为全市有一半左右的学生能够达到,你认为标准成绩分别定为多少?说明理由;按拟定的合格标准,估计该市4650人中有多少人在合格以上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=90°,AB=BC=10 cm,点P从A出发沿射线AB以1cm/s的速度作直线运动,点Q从C出发沿边BC的延长线以2cm/s的速度作直线运动,如果P,Q分别从A,B同时出发,经过_____秒,△PCQ的面积为24 cm2?

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)
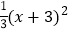 =3.
=3.(2)(y+2)2=(3y﹣1)2.
(3)(x﹣2)(x+5)=8.
(4)(2x+1)2=﹣6x﹣3.
(5)2x2﹣3x﹣2=0.
(6)4x2﹣12x﹣1=0(配方法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某中学第八届校园文化艺术节中,其中有三个年级老师参加的“校园歌手大奖赛”,艺术节组委会要求三个年级先进行预赛,选出男、女各一名选手参加决赛,七、八、九年级选手编号分别为男1号,女1号;男2号,女2号;男3号,女3号,比赛规则是男女各一人组成搭档进行决赛比赛.
(1)求是同一年级男、女教师选手组成搭档的概率.
(2)求低年级男教师与高年级女教师组成搭档的概率.
相关试题

