搜索
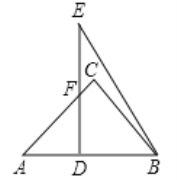
【题目】如图，将两块三角板重叠放置，其中∠C=∠BDE=90°，∠A=45°，∠E=30°，AB=DE=6，求重叠部分四边形DBCF的面积。
参考答案：
【答案】
【解析】
观察可看出，所求四边形的面积等于等腰直角三角形的面积减去S△ADF，从而只要求出这两个三角形的面积即可，这要求我们综合利用解直角三角形，直角三角形的性质和三角函数的灵活运用来解答．
解：在△EDB中，
∵∠BDE=90°，∠E=30°，DE=6，
∴DB=DEtan30°=6×
=2
，
∴AD=AB-DB=6-2．
又∵∠A=45°，∠AFD=45°，得FD=AD．
∴S△ADF=
AD2=×（6-2）2=24-12．
在等腰直角三角形ABC中，斜边AB=6，
∴AC=BC=3
，
∴S△ABC=AC2=9，
∴S四边形DBCF=S△ABC-S△ADF=9-（24-12）=12-15．
故答案为： ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知⊙O的半径为10，圆心O到弦AB的距离为5，则弦AB所对的圆周角的度数是（ ）
A. 30° B. 60° C. 30°或150° D. 60°或120°
-
科目： 来源： 题型：
查看答案和解析>>【题目】作图题：要求尺规作图，不写作法，保留作图痕迹，写出结论。
(1)如图所示，104国道OA和327国道OB在曲阜市相交于O点，在∠AOB的内部有工厂C和D，现要建一个货站P，使P到OA和OB的距离相等，且使PC=PD，用尺规作出P点的位置；
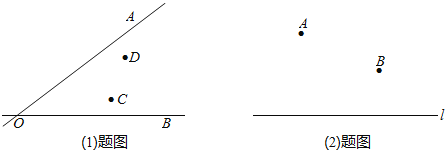
(2)在图中直线上找到一点M，使它到A、B两点的距离和最小。
-
科目： 来源： 题型：
查看答案和解析>>【题目】若将一幅三角板按如图所示的方式放置，则下列结论中不正确的是( )
A. ∠1＝∠3 B. 如果∠2＝30°，则有AC∥DE
C. 如果∠2＝30°，则有BC∥AD D. 如果∠2＝30°，必有∠4＝∠C
-
科目： 来源： 题型：
查看答案和解析>>【题目】将一幅三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．
（1）求证：CF∥AB．
（2）求∠DFC的度数．
-
科目： 来源： 题型：
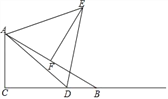
查看答案和解析>>【题目】在Rt△ABC中，∠C=90°，∠B=30°，AB=10，点D是射线CB上的一个动点，△ADE是等边三角形，点F是AB的中点，连接EF．
（1）如图，点D在线段CB上时，
①求证：△AEF≌△ADC；
②连接BE，设线段CD=x，BE=y，求y2﹣x2的值；
（2）当∠DAB=15°时，求△ADE的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，ABCD的对角线AC、BD交于点O，DE平分∠ADC交AB于点E，∠BCD=60°，AD=
AB，连接OE．下列结论：①SABCD=ADBD；②DB平分∠CDE；③AO=DE；④S△ADE=5S△OFE，其中正确的个数有（ ）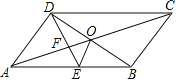
A. 1个 B. 2个 C. 3个 D. 4个
相关试题
