【题目】解答题 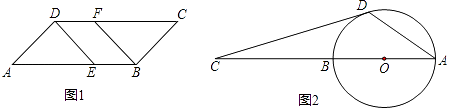
(1)如图1,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.求证:DE=BF;
(2)如图2,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,求∠CDA的度数.
参考答案:
【答案】
(1)证明:∵四边形ABCD是ABCD,
∴AB∥CD,AB=CD,
∵AE=CF,
∴BE=DF,
∴四边形BEDF是平行四边形,
∴DE=BF;
(2)解:连接OD,
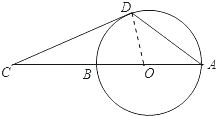
则∠ODC=90°,∠COD=70°;
∵OA=OD,
∴∠ODA=∠A= ![]() ∠COD=35°,
∠COD=35°,
∴∠CDA=∠CDO+∠ODA=90°+35°=125°.
【解析】(1)根据平行四边形的性质可证AB∥CD,AB=CD,又由已知可证BE=DF,即证四边形BEDF是平行四边形,故DE=BF;(2)连接OD,构造直角三角形,利用OA=OD,可求得∠ODA=35°,从而根据∠CDA=∠CDO+∠ODA计算求解.
【考点精析】关于本题考查的平行四边形的性质和切线的性质定理,需要了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A为函数y=
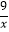 (x>0)图象上一点,连结OA,交函数y=
(x>0)图象上一点,连结OA,交函数y= 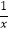 (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 .
(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 . 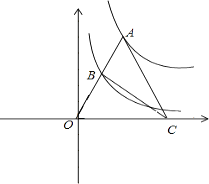
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的横线内.
-2.4,3,2.018,1,-0.15,0,-(-2.28),-
 ,-|-4|.
,-|-4|.正数:________________________;
负有理数:______________________;
整数:__________________________;
负分数:________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下面各题
(1)化简:a(a﹣2b)+(a+b)2
(2)解不等式组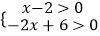 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生体育训练的情况,某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试(把成绩结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:

(1)求本次抽样测试的学生人数;
(2)求扇形图中∠α的度数,并把条形统计图补充完整;
(3)该市九年级共有学生9000名,如果全部参加这次体育测试,则测试等级为D的约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=
 过点A(2,4),B(0,3)、题目中的矩形部分是一段因墨水污染而无法辨认的文字.
过点A(2,4),B(0,3)、题目中的矩形部分是一段因墨水污染而无法辨认的文字.(1)根据现有的信息,请求出题中的一次函数的解析式.
(2)根据关系式画出这个函数图象.
(3)过点B能不能画出一直线BC将△ABO(O为坐标原点)分成面积比为1:2的两部分?如能,可以画出几条,并求出其中一条直线所对应的函数关系式,其它的直接写出函数关系式;若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点D在反比例函数y=
 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=  .
.
(1)求反比例函数y= 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
相关试题

