【题目】如图,点A为函数y= ![]() (x>0)图象上一点,连结OA,交函数y=
(x>0)图象上一点,连结OA,交函数y= ![]() (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 .
(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 . 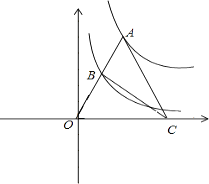
参考答案:
【答案】6
【解析】解:设点A的坐标为(a, ![]() ),点B的坐标为(b,
),点B的坐标为(b, ![]() ), ∵点C是x轴上一点,且AO=AC,
), ∵点C是x轴上一点,且AO=AC,
∴点C的坐标是(2a,0),
设过点O(0,0),A(a, ![]() )的直线的解析式为:y=kx,
)的直线的解析式为:y=kx,
∴ ![]() ,
,
解得,k= ![]() ,
,
又∵点B(b, ![]() )在y=
)在y= ![]() 上,
上,
∴ ![]() ,解得,
,解得, ![]() 或
或 ![]() (舍去),
(舍去),
∴S△ABC=S△AOC﹣S△OBC= ![]() =
= ![]() ,
,
故答案为:6.
根据题意可以分别设出点A、点B的坐标,根据点O、A、B在同一条直线上可以得到A、B的坐标之间的关系,由AO=AC可知点C的横坐标是点A的横坐标的2倍,从而可以得到△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
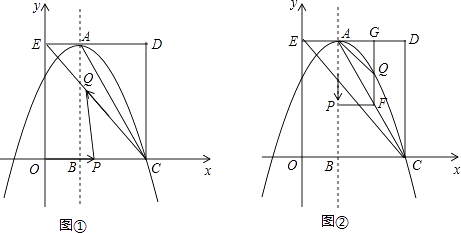
(1)填空:点A坐标为;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少? -
科目: 来源: 题型:
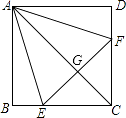
查看答案和解析>>【题目】如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE , 其中结论正确的个数为( )
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a﹣b+c≥0;
④ 的最小值为3.
的最小值为3.
其中,正确结论的个数为( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的横线内.
-2.4,3,2.018,1,-0.15,0,-(-2.28),-
 ,-|-4|.
,-|-4|.正数:________________________;
负有理数:______________________;
整数:__________________________;
负分数:________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下面各题
(1)化简:a(a﹣2b)+(a+b)2
(2)解不等式组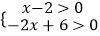 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
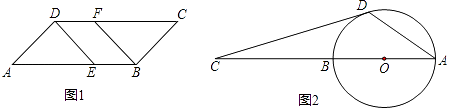
(1)如图1,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.求证:DE=BF;
(2)如图2,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,求∠CDA的度数.
相关试题

