【题目】如图, ![]() ,
, ![]() 、
、![]() 、
、![]() 分别平分
分别平分![]() 的内角
的内角![]() 、外角
、外角![]() 、外角
、外角![]() .以下结论:①
.以下结论:①![]() ∥
∥![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 平分
平分![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
参考答案:
【答案】C
【解析】分析:(1)说明∠9=∠ABC;(2)说明∠2+∠3=90°;(3)说明∠BDC=![]() ∠BAC,而
∠BAC,而![]() ∠BAC+∠ABC=90°;(4)由∠BEC=90°-
∠BAC+∠ABC=90°;(4)由∠BEC=90°-![]() ∠BAC判断;(5)由∠BDC=
∠BAC判断;(5)由∠BDC=![]() ∠BAC,∠ADB=
∠BAC,∠ADB=![]() ∠ABC,而∠BAC与∠ABC不一定相等.
∠ABC,而∠BAC与∠ABC不一定相等.
详解:如图,由题意可知,∠1=∠2,∠3=∠4,∠5=∠6=∠7,∠8=∠9,∠ABC=∠ACB.
①因为∠8+∠9=∠ABC+∠ACB,∠ABC=∠ACB,∠8=∠9,
所以2∠9=2∠ABC,所以∠9=∠ABC,所以AD∥BC,则①正确;
②因为,∠1=∠2,∠3=∠4,,∠1+∠2+∠3+∠4=180°,
所以∠2+∠3=90°,所以DB⊥BE,则②正确;
③因为∠6=∠2+∠BDC,2∠6=2∠2+∠BAC,
所以2(∠2+∠BDC)=2∠2+∠BAC,即∠BDC=![]() ∠BAC,
∠BAC,
因为∠BAC+∠ABC+∠ACB=180°,所以![]() ∠BAC+∠ABC=90°,
∠BAC+∠ABC=90°,
即∠BDC+∠ABC=90°,则③正确;
④因为2∠3=∠A+∠ACB,2∠7=∠A+∠ABC,∠BEC=180°-(∠3+∠7),
所以∠BEC=180°-![]() (∠A+∠ACB+∠A+∠ABC)=90°-
(∠A+∠ACB+∠A+∠ABC)=90°-![]() ∠BAC,
∠BAC,
所以∠BAC+2∠BEC=180°,则④正确;
⑤因为AD∥BC,所以∠ADB=∠2,即∠ADB=![]() ∠ABC,
∠ABC,
因为∠BDC=![]() ∠BAC,∠BAC与∠ABC不一定相等,
∠BAC,∠BAC与∠ABC不一定相等,
所以∠BDC与∠ADB不一定相等,则⑤错误.
故选C.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC, ∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=132°,∠BGC=118°,则∠A的度数为( )

A. 65° B. 66° C. 70° D. 78°
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)在给定方格纸中画出平移后的△A′B′C′;
利用网格点和三角板画图或计算:
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明与小红开展读书比赛.小明找出了一本以前已读完84页的古典名著打算继续往下读,小红上个周末恰好刚买了同一版本的这本名著,不过还没开始读.于是,两人开始了读书比赛.他们利用下表来记录了两人5天的读书进程.

例如,第5天结束时,小明还领先小红24页,此时两人所读到位置的页码之和为424.已知两人各自每天所读页数相同.
(1)表中空白部分从左到右2个数据依次为____,_____;
(2)小明、小红每人每天各读多少页?
-
科目: 来源: 题型:
查看答案和解析>>【题目】当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移后得△DEF,使点A的对应点为点D,点B的对应点为点E.
(1)画出△DEF;
(2)连接AD、BE,则线段AD与BE的关系是 ;
(3)求△DEF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC中, BD平分∠ABC,且与△ABC的外角∠ACE的角平分线交于点D.
(1)若
 ,
,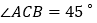 ,求∠D的度数;
,求∠D的度数;(2)若把∠A截去,得到四边形MNCB,如图②,猜想∠D、∠M、∠N的关系,并说明理由.

相关试题

