【题目】在菱形ABCD中,P是AB上一动点(但不与A、B两点重合),DP的延长线交CB延长线于点E.
(1)△APD与△BPE是否总相似,为什么?
(2)当P为AB中点时,求证:点B是EC中点.
(3)当PD⊥AB时,设AD=10,sinA=![]() ,求BE的长.
,求BE的长.

参考答案:
【答案】(1)相似.理由见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)由四边形ABCD为菱形,得到AD∥BC,即可得到结论;(2)先由角角边证得△APD≌△BPE,AD=BE,再由四边形ABCD为菱形, 得到AD=BC,即BE=BC,即点B为EC中点.(3)再Rt△APD中,由AD=10,sinA=![]() 得PD=8,AP=6,故PB=4,由△APD∽△BPE可得
得PD=8,AP=6,故PB=4,由△APD∽△BPE可得![]() =
=![]() ,即可求得BE长.
,即可求得BE长.
试题解析:: (1)相似.
∵四边形ABCD为菱形,
∴AD∥BC.
∴∠DAP=∠EBP,∠ADP=∠BEP.
∴△APD△BPE.
(2)∵P是AB中点,
∴AP=BP.
又∵∠DAP=∠EBP,∠ADP=∠BEP,
∴△APD≌△BPE.
∴AD=BE.
∵四边形ABCD为菱形,
∴AD=BC.
∴BE=BC.
即点B为EC中点.
(3)∵PD⊥AB,AD=10,sinA=![]() . ∴PD=8.∴AP=6.∴PB=AB—AP=10—6=4.
. ∴PD=8.∴AP=6.∴PB=AB—AP=10—6=4.
∵△APD∽△BPE,∴ ![]() =
=![]() ∴BE=
∴BE=![]() =
=![]() =
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论: ①快递车从甲地到乙地的速度为100千米/时;
②甲、乙两地之间的距离为120千米;
③图中点B的坐标为(3 ,75);
,75);
④快递车从乙地返回时的速度为90千米/时,
以上4个结论正确的是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2018次相遇在___边上.
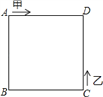
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2﹣2向上平移4个单位,再向右平移3个单位,得到新的抛物线,那么新的抛物线的表达式是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 的对称轴为
的对称轴为 轴,且经过(0,0),(
轴,且经过(0,0),( )两点,点P在抛物线上运动,以P为圆心的⊙P经过定点A(0,2),
)两点,点P在抛物线上运动,以P为圆心的⊙P经过定点A(0,2),(1)求
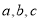 的值;
的值; (2)求证:点P在运动过程中,⊙P始终与
 轴相交;
轴相交;(3)设⊙P与
 轴相交于M
轴相交于M ,N
,N  (
( <
<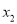 )两点,当△AMN为等腰三角形时,求圆心P的纵坐标.
)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.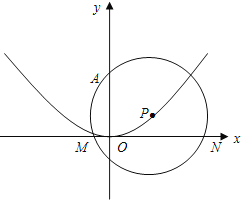
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=115°,∠EOF =155°,OA平分∠EOC,OB平分∠DOF,

(1)求∠AOE+∠FOB度数;
(2)求∠COD度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程6x-9=10x-45与方程3a-1=3(x+a)-2a的解相同
(1)求这个相同的解;
(2)求a的值;
(3)若[m]表示不大于m的最大整数,求[
 -2]的值
-2]的值
相关试题

