【题目】已知如图,在△ABC中,以AB、AC为直角边, 分别向外作等腰直角三角形ABE、ACF,连结EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.
(1)用圆规比较EM与FM的大小.
(2)你能说明由(1)中所得结论的道理吗?

参考答案:
【答案】(1)EM=FM;(2)证明见解析.
【解析】
(1)直接用圆规比较两线段的大小;(2)作EH⊥AM,垂足为H,FK⊥AM,垂足为K.先说明Rt△EHA≌Rt△ADB, 得EH=AD,Rt△FKA≌Rt△ADC, 得FK=AD,得EH=FK,在Rt△EHK与Rt△FKM中,Rt△EHM≌Rt△FKM,得EM=FM.
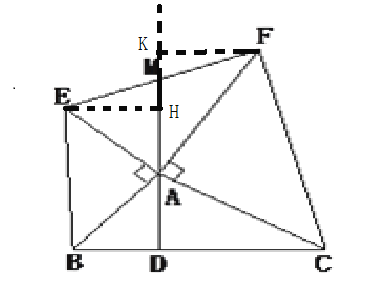
解:(1)EM=FM
(2)作EH⊥AM,垂足为H,FK⊥AM,垂足为K,则∠AHE=90,∠AKF=90,
因为,AD⊥BC,
所以,∠ADB=90,
所以,∠ABD+∠BAD=90,
又因为,△ABE是等腰直角三角形,
所以,AE=AB,∠BAE=90,
所以,∠EAH+∠BAD=90,
所以,∠EAH=∠ABD,
所以,Rt△EHA≌Rt△ADB(AAS),
所以,EH=AD,
同理:
Rt△FKA≌Rt△ADC, FK=AD,
所以EH=FK
在Rt△EHK与Rt△FKM中,
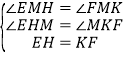
所以,Rt△EHM≌Rt△FKM(AAS)
得EM=FM.
-
科目: 来源: 题型:
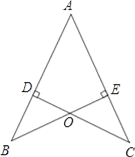
查看答案和解析>>【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律:观察下面由组成的图案和算式,解答问题:
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请计算 1+3+5+7+9+11;
(2)请计算 1+3+5+7+9+…+19;
(3)请计算 1+3+5+7+9+…+(2n﹣1);
(4)请用上述规律计算:21+23+25+…+99.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若数 a,b 在数轴上的位置如图所示,则下列各式中一定成立的是( )
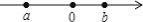
A. ﹣a>b B. a+b>0 C. a﹣b>a+b D. |a|+|b|<|a+b|
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2016年体育中考中,某班一学习小组6名学生的体育成绩如下表,则这组学生的体育成绩的众数,中位数,方差依次为( )
成绩(分)
27
28
30
人数
2
3
1
A.28,28,1
B.28,27.5,1
C.3,2.5,5
D.3,2,5 -
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A.3
B.5
C.2或3
D.3或5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )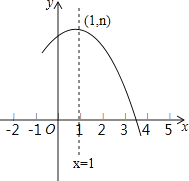
A.1
B.2
C.3
D.4
相关试题

