【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

参考答案:
【答案】(1)30°;(2)8.
【解析】
(1)由在△ABC中,AB=AC,∠A=40°,利用等腰三角形的性质,即可求得∠ABC的度数,然后由AB的垂直平分线MN交AC于点D,根据线段垂直平分线的性质,可求得AD=BD,继而求得∠ABD的度数,则可求得∠DBC的度数;
(2)根据AE=6,AB=AC,得出CD+AD=12,由△CBD的周长为20,代入即可求出答案.
(1)∵在△ABC中,AB=AC,∠A=40°,
∴∠ABC=∠C=70°,
∵AB的垂直平分线MN交AC于点D,
∴AD=BD,
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=30°;
(2)∵AE=6,
∴AC=AB=2AE=12,
∵△CBD的周长为20,
∴BC=20﹣(CD+BD)=20﹣(CD+AD)=20﹣12=8,
∴BC=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列命题
①一组对边平行,一组对角相等的四边形是平行四边形.
②两组对角分别相等的四边形是平行四边形.
③一组对边相等,一组对角相等的四边形是平行四边形.
④一组对边平行,一条对角线被另一条对角线平分的四边形是平行四边形.
(1)上述四个命题中,是真命题的是 (填写序号);
(2)请选择一个真命题进行证明.(写出已知、求证,并完成证明)
已知: .
求证: .
证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3),B(﹣3,1),C(﹣1,3).
(1)请按下列要求画图:
①平移△ABC,使点A的对应点A1的坐标为(﹣4,﹣3),请画出平移后的△A1B1C1;
②△A2B2C2与△ABC关于原点O中心对称,画出△A2B2C2.
(2)若将△A1B1C1绕点M旋转可得到△A2B2C2,请直接写出旋转中心M点的坐标 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生对篮球、羽毛球、乒乓球、踢毽子、跳绳等5项体育活动的喜欢程度,某校随机抽查部分学生,对他们最喜欢的体育项目(每人只选一项)进行了问卷调查,并将统计数据绘制成如下两幅不完整的统计图:
请解答下列问题:
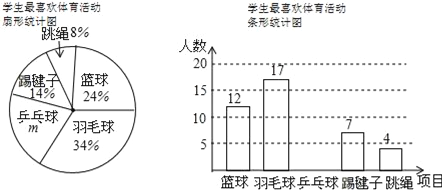
(1)m= %,这次共抽取了 名学生进行调查;请补全条形统计图;
(2)若全校有800名学生,则该校约有多少名学生喜爱打篮球?
(3)学校准备从喜欢跳绳活动的4人(二男二女)中随机选取2人进行体能测试,求抽到一男一女学生的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴的单位长度为1,点
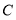 ,
,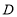 表示的数互为相反数,结合数轴回答下列问题:
表示的数互为相反数,结合数轴回答下列问题:
(1)请在数轴上标出原点
 的位置.
的位置.(2)直接写出点
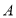 ,
,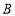 ,
,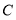 ,
,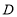 所表示的数,并判断哪一点表示的数的平方最大,最大是多少?
所表示的数,并判断哪一点表示的数的平方最大,最大是多少?(3)从A,B两题中任选一题作答.
A. ①若点
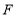 在数轴上,与点
在数轴上,与点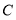 的距离
的距离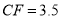 ,求点
,求点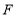 表示的数;
表示的数;②设动点
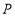 从点
从点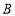 出发,以每秒3个单位长度的速度沿数轴的正方向匀速向终点
出发,以每秒3个单位长度的速度沿数轴的正方向匀速向终点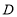 运动,运动时间为
运动,运动时间为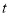 秒,求点
秒,求点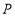 ,
,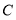 之间的距离
之间的距离 .(用含
.(用含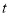 的代数式表示)
的代数式表示)B.设点
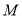 ,
,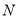 都从点
都从点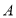 出发沿数轴的正方向匀速向终点
出发沿数轴的正方向匀速向终点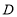 运动.点
运动.点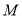 的速度为每秒2个单位长度,点
的速度为每秒2个单位长度,点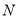 的速度为每秒5个单位长度,当点
的速度为每秒5个单位长度,当点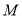 运动到点
运动到点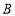 时点
时点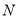 开始运动,设点
开始运动,设点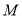 运动的时间为
运动的时间为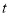 秒,求点
秒,求点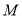 ,
,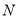 之间的距离
之间的距离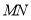 .(用含
.(用含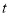 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
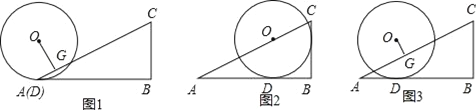
查看答案和解析>>【题目】如图,△ABC中,∠B=90°,tan∠BAC=
 ,半径为2的⊙O从点A开始(图1),沿AB向右滚动,滚动时始终与AB相切(切点为D);当圆心O落在AC上时滚动停止,此时⊙O与BC相切于点E(图2).作OG⊥AC于点G.
,半径为2的⊙O从点A开始(图1),沿AB向右滚动,滚动时始终与AB相切(切点为D);当圆心O落在AC上时滚动停止,此时⊙O与BC相切于点E(图2).作OG⊥AC于点G.(1)利用图2,求cos∠BAC的值;
(2)当点D与点A重合时(如图1),求OG;
(3)如图3,在⊙O滚动过程中,设AD=x,请用含x的代数式表示OG,并写出x的取值范围.
-
科目: 来源: 题型:
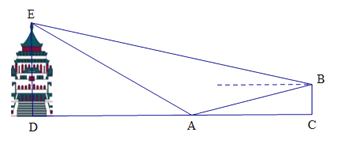
查看答案和解析>>【题目】气魄雄伟的大礼堂座落在渝中区学田湾,它是一座仿古民族建筑.“五一”期间,小明和妈妈到重庆大礼堂参观游玩.参观结束后,穿过人民广场到达A处,回望礼堂,更显气势雄伟,金碧辉煌.此时,在A点观察到礼堂顶端的仰角为30°,沿着坡度为1:3的斜坡AB走一段距离到达B点,观察到礼堂顶端 的仰角是22°,测得点A与BC之间的水平距离
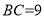 米,则大礼堂的高度DE为( )米.(精确到1米.参考数据:
米,则大礼堂的高度DE为( )米.(精确到1米.参考数据:  ,
, 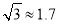 .)
.)
A. 58 B. 60 C. 62 D. 64
相关试题

