搜索
【题目】如果不等式
有解,那么m的取值范围是( )
A.m>7
B.m≥7
C.m<7
D.m≤7
参考答案：
【答案】C
【解析】解出不等式组的解集，与不等式组
有解相比较，得到m的取值范围．
由（1)得x＜7，
由（2)得x＞m，
∵不等式组有解，
∴m＜x＜7；
∴m＜7，
故选C．
【考点精析】根据题目的已知条件，利用不等式的解集和一元一次不等式组的解法的相关知识可以得到问题的答案，需要掌握一个含有未知数的不等式的所有解，组成这个不等式的解集（即未知数的取值范围）；解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一组数据－3，x，－2，3,1,6的中位数是1，则其众数为________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为“方便交通，绿色出行”，人们常选择以共享单车作为代步工具、图（1）所示的是一辆自行车的实物图．图（2）是这辆自行车的部分几何示意图，其中车架档AC与CD的长分别为45cm和60cm，且它们互相垂直，座杆CE的长为20cm．点A、C、E在同一条直线上，且∠CAB=75°．
（参考数据：sin75°=0.966，cos75°=0.259，tan75°=3.732）
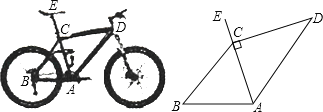
图（1） 图（2）
（1）求车架档AD的长；
（2）求车座点E到车架档AB的距离（结果精确到1cm）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在Rt△ABC中，∠ACB=90°，cosB=
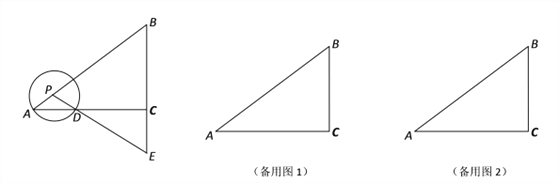
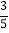，BC=3，P是射线AB上的一个动点，以P为圆心，PA为半径的⊙P与射线AC的另一个交点为D，直线PD交直线BC于点E．（1）当PA=1时，求CE的长；
（2）如果点P在边AB的上，当⊙P与以点C为圆心，CE为半径的⊙C内切时，求⊙P的半径；
（3）设线段BE的中点为Q，射线PQ与⊙P相交于点F，点P在运动过程中，当PE∥CF时，求AP的长．
-
科目： 来源： 题型：
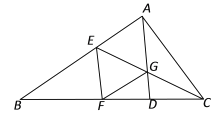
查看答案和解析>>【题目】如图，点D、E分别是△ABC边BC、AB上的点，AD、CE相交于点G，过点E作EF∥AD交BC于点F，且
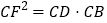，联结FG.（1）求证：GF∥AB；
（2）如果∠CAG=∠CFG，求证：四边形AEFG是菱形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】点P（m+3，m+1）在直角坐标系的x轴上，则P点的坐标为（ ）
A.（0，﹣2）
B.（2，0）
C.（0，2）
D.（0，﹣4） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图是某品牌太阳能热水器的实物图和横断面示意图，已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心，支架CD与水平面AE垂直，AB＝110厘米，∠BAC＝37°，垂直支架CD=57厘米，DE是另一根辅助支架，且∠CED＝60°.
（1）求辅助支架DE长度；(结果保留根号)
（2）求水箱半径OD的长度．(结果精确到1厘米，参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）
相关试题
