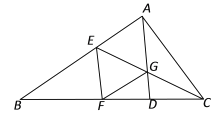
【题目】如图,点D、E分别是△ABC边BC、AB上的点,AD、CE相交于点G,过点E作EF∥AD交BC于点F,且![]() ,联结FG.
,联结FG.
(1)求证:GF∥AB;
(2)如果∠CAG=∠CFG,求证:四边形AEFG是菱形.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由![]() ,可得
,可得![]() ,再由EF∥AD,根据平行线分线段成比例定理可得
,再由EF∥AD,根据平行线分线段成比例定理可得 ![]() ,所以
,所以![]() ,即可得GF∥AB ;(2)联结AF ,证明ΔCAD∽ΔCBA,根据相似三角形的性质可得
,即可得GF∥AB ;(2)联结AF ,证明ΔCAD∽ΔCBA,根据相似三角形的性质可得 ![]() ,即
,即![]() ,再因
,再因![]() ,即可得
,即可得![]() ,可得∠CAF=∠CFA,因∠CAG=∠CFG,可得∠GAF=∠GFA,即可得GA=GF,再由四边形AEFG是平行四边形,即可判断四边形AEFG是菱形.
,可得∠CAF=∠CFA,因∠CAG=∠CFG,可得∠GAF=∠GFA,即可得GA=GF,再由四边形AEFG是平行四边形,即可判断四边形AEFG是菱形.
试题解析:
(1)证明:∵![]() ,∴
,∴![]()
∵EF∥AD,∴ ![]()
∴![]()
∴GF∥AB
(2) 联结AF ,∵GF∥AB ∴![]()
∵![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ∽
∽![]()
∴ ![]() ,即
,即![]()
∵![]() ,∴
,∴![]()
∴![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]()
∵GF∥AB,EF∥AD,∴四边形![]() 是平行四边形
是平行四边形
∴四边形![]() 是菱形
是菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】为“方便交通,绿色出行”,人们常选择以共享单车作为代步工具、图(1)所示的是一辆自行车的实物图.图(2)是这辆自行车的部分几何示意图,其中车架档AC与CD的长分别为45cm和60cm,且它们互相垂直,座杆CE的长为20cm.点A、C、E在同一条直线上,且∠CAB=75°.
(参考数据:sin75°=0.966,cos75°=0.259,tan75°=3.732)
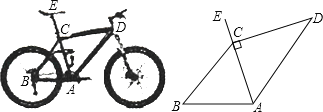
图(1) 图(2)
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离(结果精确到1cm).
-
科目: 来源: 题型:
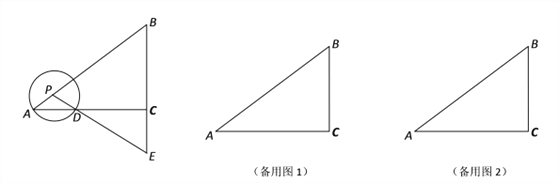
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ACB=90°,cosB=
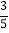 ,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.(1)当PA=1时,求CE的长;
(2)如果点P在边AB的上,当⊙P与以点C为圆心,CE为半径的⊙C内切时,求⊙P的半径;
(3)设线段BE的中点为Q,射线PQ与⊙P相交于点F,点P在运动过程中,当PE∥CF时,求AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果不等式
 有解,那么m的取值范围是( )
有解,那么m的取值范围是( )
A.m>7
B.m≥7
C.m<7
D.m≤7 -
科目: 来源: 题型:
查看答案和解析>>【题目】点P(m+3,m+1)在直角坐标系的x轴上,则P点的坐标为( )
A.(0,﹣2)
B.(2,0)
C.(0,2)
D.(0,﹣4) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心,支架CD与水平面AE垂直,AB=110厘米,∠BAC=37°,垂直支架CD=57厘米,DE是另一根辅助支架,且∠CED=60°.
(1)求辅助支架DE长度;(结果保留根号)
(2)求水箱半径OD的长度.(结果精确到1厘米,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校准备组织520名学生进行野外考察活动,行李共有240件.学校计划租用甲、乙两种型号的汽车共12辆,经了解,甲种汽车每辆最多能载50人和15件行李,乙种汽车每辆最多能载40人和25件行李.设租用甲种汽车
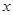 辆,你认为下列符合题意的不等式组是( )
辆,你认为下列符合题意的不等式组是( )
A.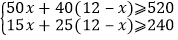
B.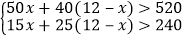
C.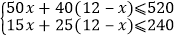
D.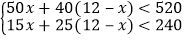
相关试题

