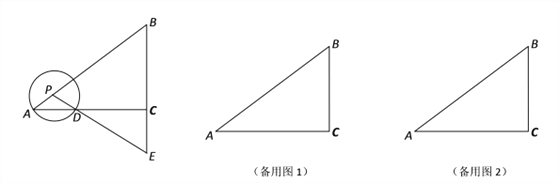
【题目】如图,已知在Rt△ABC中,∠ACB=90°,cosB=![]() ,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
,BC=3,P是射线AB上的一个动点,以P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
(1)当PA=1时,求CE的长;
(2)如果点P在边AB的上,当⊙P与以点C为圆心,CE为半径的⊙C内切时,求⊙P的半径;
(3)设线段BE的中点为Q,射线PQ与⊙P相交于点F,点P在运动过程中,当PE∥CF时,求AP的长.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)作PH⊥AC,垂足为H,由垂径定理可得AH=DH,由cosB=![]() BC=3,可得AB=5,AC=4,再由PH∥BC,可得
BC=3,可得AB=5,AC=4,再由PH∥BC,可得![]() ,代入数据求得PH=
,代入数据求得PH=![]() ,即可求得
,即可求得![]() ,由
,由![]() ,代入数据求得CE的长即可;(2)当⊙P与⊙C内切时,点C在⊙P内,可得点D在AC的延长线上,过点P作PG⊥AC,垂足为G,设PA=
,代入数据求得CE的长即可;(2)当⊙P与⊙C内切时,点C在⊙P内,可得点D在AC的延长线上,过点P作PG⊥AC,垂足为G,设PA=![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,根据
,根据![]() ,代入数据可得
,代入数据可得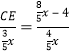 ,解得
,解得![]() ,因⊙P与⊙C内切,即可得
,因⊙P与⊙C内切,即可得![]() ,所以
,所以![]() ,即
,即![]() ,解得
,解得![]() ,
,![]() (舍去),即当⊙P与⊙C内切时,⊙P的半径为
(舍去),即当⊙P与⊙C内切时,⊙P的半径为![]() ;(3)先证明四边形PDCF是平行四边形,可得PF=CD,再分当点P在边AB的上和当点P在边AB的延长线上两种情况求AP的长.
;(3)先证明四边形PDCF是平行四边形,可得PF=CD,再分当点P在边AB的上和当点P在边AB的延长线上两种情况求AP的长.
试题解析:
(1)作PH⊥AC,垂足为H,∵PH过圆心,∴AH=DH
∵∠ACB=90°,∴PH∥BC, ∵cosB=![]() ,BC=3,∴AB=5,AC=4
,BC=3,∴AB=5,AC=4
∵PH∥BC,∴![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]()
∴DC=![]() ,又∵
,又∵![]() ,∴
,∴![]() ,∴
,∴![]()
(2)当⊙P与⊙C内切时,点C在⊙P内,∴点D在AC的延长线上
过点P作PG⊥AC,垂足为G,设PA=![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() ,∵
,∵![]() ,
,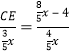 ,
,![]() …(1分)
…(1分)
∵⊙P与⊙C内切,∴![]()
∴![]()
∴![]() ,∴
,∴![]() ,
,![]() (舍去)
(舍去)
∴当⊙P与⊙C内切时,⊙P的半径为![]() .
.
(3)∵∠ABC+∠A=90゜,∠PEC+∠CDE=90゜,∠A=∠PDA,
∴∠ABC=∠PEC
∵∠ABC=∠EBP,
∴∠PEC=∠EBP,
∴PB=PE
∵点Q为线段BE的中点,
∴PQ⊥BC,∴PQ∥AC
∴当PE∥CF时,四边形PDCF是平行四边形,∴PF=CD
当点P在边AB的上时,![]() ,
,![]()
当点P在边AB的延长线上时,![]() ,
,![]()
综上所述,当PE∥CF时,AP的长为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级二班在订购本班的班服前,按身高型号进行登记,对女生的记录中,身高150cm以下记为S号,150160cm以下记为M号,160170cm以下记为L号.170cm 以上记为XL号.若用统计图描述这些数据,合适的统计图是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据-3,x,-2,3,1,6的中位数是1,则其众数为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为“方便交通,绿色出行”,人们常选择以共享单车作为代步工具、图(1)所示的是一辆自行车的实物图.图(2)是这辆自行车的部分几何示意图,其中车架档AC与CD的长分别为45cm和60cm,且它们互相垂直,座杆CE的长为20cm.点A、C、E在同一条直线上,且∠CAB=75°.
(参考数据:sin75°=0.966,cos75°=0.259,tan75°=3.732)
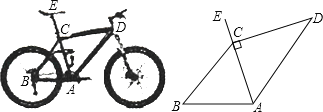
图(1) 图(2)
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离(结果精确到1cm).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果不等式
 有解,那么m的取值范围是( )
有解,那么m的取值范围是( )
A.m>7
B.m≥7
C.m<7
D.m≤7 -
科目: 来源: 题型:
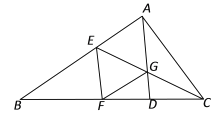
查看答案和解析>>【题目】如图,点D、E分别是△ABC边BC、AB上的点,AD、CE相交于点G,过点E作EF∥AD交BC于点F,且
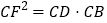 ,联结FG.
,联结FG.(1)求证:GF∥AB;
(2)如果∠CAG=∠CFG,求证:四边形AEFG是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(m+3,m+1)在直角坐标系的x轴上,则P点的坐标为( )
A.(0,﹣2)
B.(2,0)
C.(0,2)
D.(0,﹣4)
相关试题

