【题目】一个不透明的口袋里装有分别标有汉字“幸”、“福”、“济”、“宁”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“福”的概率为多少?
(2)小颖从中任取一球,记下汉字后放回袋中,然后再从中任取一球,求小颖取出的两个球上汉字恰能组成“幸福”或“济宁”的概率.
参考答案:
【答案】
(1)解:∵一个不透明的口袋里装有分别标有汉字“幸”、“福”、“济”、“宁”的四个小球,除汉字不同之外,小球没有任何区别,
∴从中任取一个球,球上的汉字刚好是“福”的概率为: ![]() ;
;
(2)解:画树状图得:

∵共有16种等可能的结果,小颖取出的两个球上汉字恰能组成“幸福”或“济宁”的有4种情况,
∴小颖取出的两个球上汉字恰能组成“幸福”或“济宁”的概率为: ![]() =
= ![]() .
.
【解析】(1)由一个不透明的口袋里装有分别标有汉字“幸”、“福”、“济”、“宁”的四个小球,直接利用概率公式求解即可求得答案;(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小颖取出的两个球上汉字恰能组成“幸福”或“济宁”的情况,再利用概率公式即可求得答案.
【考点精析】根据题目的已知条件,利用列表法与树状图法的相关知识可以得到问题的答案,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式
(1)2cos45°+sin30°cos60°+cos30°
(2)|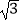 ﹣5|+2cos30°+(
﹣5|+2cos30°+(  )﹣1+(9﹣
)﹣1+(9﹣ 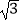 )0+
)0+  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=60°,为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造,经地质人员勘测,当坡角不超过45°时,可确保山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC削进到E处,问BE至少是多少米?(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 的图象与一次函数y=kx﹣3的图象在第一象限内相交于点A,且点A的横坐标为4.
的图象与一次函数y=kx﹣3的图象在第一象限内相交于点A,且点A的横坐标为4. 
(1)求点A的坐标及一次函数的解析式;
(2)若直线x=2与反比例函数和一次函数的图象分别交于点B、C,求线段BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,AE为⊙O的切线,若tan∠ABE=
 ,AE=3,求BD的长.
,AE=3,求BD的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F.
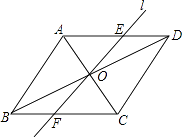
(1)求证:△AOE≌△COF;
(2)当α=30°时,求线段EF的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.

(1)求∠CDO的度数;
(2)求出点F坐标的表达式(用含t的代数式表示);
(3)当S△COD﹣S四边形COAF=7时,求抛物线解析式;
(4)当以B,C,O三点为顶点的三角形与△CEF相似时,请直接写出t的值.
相关试题

