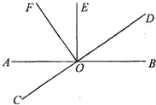
【题目】如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
(1)图中∠AOF的余角有 ;(把符合条件的角都填出来)
(2)如果∠AOD=140°,那么根据 ,可得∠BOC= 度;
(3)已知5∠EOF=∠AOD,求∠EOF的度数.
参考答案:
【答案】(1)∠EOF,∠AOC,∠BOD; (2)对顶角相等,140;(3)∠EOF=30°.
【解析】
(1)根据余角的定义、性质,可得答案;
(2)根据对顶角的性质,可得答案;
(3)根据余角的性质,可得∠EOF与∠BOD的关系,根据平角的定义,可得答案.
解:(1)图中∠AOF的余角有∠EOF,∠AOC,∠BOD;
(2)如果∠AOD=140°,那么根据 对顶角相等,可得∠BOC=140°;
故答案为:对顶角相等,140;
(3)∵∠EOF+AOF=90°,∠AOC+∠AOF=90°,∴∠EOF=∠AOC=∠BOD.
∵∠AOD+∠BOD=180°,5∠EOF=∠AOD∴5∠EOF+∠BOD=180°,即6∠EOF=180°,∠EOF=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形BEFG平放在一起.
(1)若两正方形的面积分别是16和9,直接写出边AE的长为 .
(2)①设正方形ABCD的边长为a,正方形BEFG的边长为b,求图中阴影部分的面积(用含a和b的代数式表示)
②在①的条件下,如果a+b=10,ab=16,求阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个包装纸盒的三视图(单位:cm)
(1)该包装纸盒的几何形状是什么?
(2)画出该纸盒的平面展开图.
(3)计算制作一个纸盒所需纸板的面积.(精确到个位)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A. 若|a|=﹣a,则 a 一 定是负数
B. 单项式 x3y2z 的系数为 1,次数是 6
C. 若 AP=BP,则点 P 是线段 AB 的中点
D. 若∠AOC=
 ∠AOB,则射线 OC 是∠AOB 的平分线
∠AOB,则射线 OC 是∠AOB 的平分线 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,贤贤同学用手工纸制作一个台灯灯罩,请画出这个几何体的左视图和俯视图.
(2)如图2,已知直线AB与CD相交于点O,EO⊥AB,OF是∠AOC的平分线,∠EOC= ∠AOC,求∠DOF的度数.
∠AOC,求∠DOF的度数.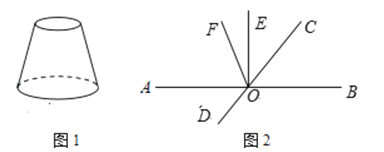
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年9月,莉莉进入八中初一,在准备开学用品时,她决定购买若干个某款笔记本,甲、乙两家文具店都有足够数量的该款笔记本,这两家文具店该款笔记本标价都是20元/个.甲文具店的销售方案是:购买该笔记本的数量不超过5个时,原价销售;购买该笔记本超过5个时,从第6个开始按标价的八折出售:乙文具店的销售方案是:不管购买多少个该款笔记本,一律按标价的九折出售.
(1)若设莉莉要购买x(x>5)个该款笔记本,请用含x的代数式分别表示莉莉到甲文具店和乙文具店购买全部该款笔记本所需的费用;
(2)在(1)的条件下,莉莉购买多少个笔记本时,到乙文具店购买全部笔记本所需的费用与到甲文具店购买全部笔记本所需的费用相同?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中, ∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.
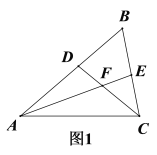
(1)如图1,若AE、CD为△ABC的角平分线. ①求证: ∠AFC=120°;②若AD=6,CE=4,求AC的长?
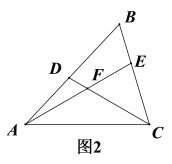
(2)如图2,若∠FAC=∠FCA=30°,求证:AD=CE.
相关试题

