【题目】如图,在ABCD中,对角线AC,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD. 
(1)求证;四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴点O是AC的中点.
又∵点E是边AB的中点,
∴OE是△ABC的中位线,
∴OE∥BC,
又∵点F在CB的延长线上,
∴OE∥BF.
∵EF∥BD,即EF∥OB,
∴四边形OBFE是平行四边形

(2)当AD⊥BD时,四边形OBFE是矩形.
理由:由(1)可知四边形OBFE是平行四边形,
又∵AD⊥BD,AD∥BC,且点F在BC的延长线上,
∴FC⊥BD,
∴∠OBF=90°,
∴四边形OBFE是矩形
【解析】(1)首先证明OE是△ABC的中位线,推出OE∥BC,由EF∥OB,推荐可提出四边形OBFE是平行四边形.(2)当AD⊥BD时,四边形OBFE是矩形. 只要证明∠EOB=90°即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时)
挖掘土石方量(单位:m3/台时)
甲型挖掘机
100
60
乙型挖掘机
120
80
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校九年级学生举行朗诵比赛,全年级学生都参加,学校对表现优异的学生进行表彰,设置一、二、三等奖各进步奖共四个奖项,赛后将九年级(1)班的获奖情况绘制成如图所示的两幅不完整的统计图,请根据图中的信息,解答下列问题:

(1)九年级(1)班共有名学生;
(2)将条形图补充完整:在扇形统计图中,“二等奖”对应的扇形的圆心角度数是;
(3)如果该九年级共有1250名学生,请估计荣获一、二、三等奖的学生共有多少名. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,∠BAC的平分线与线段BC的垂直平分线PQ相交于点P,过点P分别作PN垂直于AB于点N,PM垂直于AC于点M,BN和CM有什么数量关系?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个蓄水池,现将甲池中的水匀速注入乙池.甲、乙两个蓄水池中水的深度
 (米)与注水时间
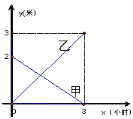
(米)与注水时间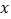 (小时)之间的关系如图5所示,根据图像提供的信息,回答下列问题:
(小时)之间的关系如图5所示,根据图像提供的信息,回答下列问题:(1)注水前甲池中水的深度是_____________米.(直接写出答案).
(2)求甲池中水的深度
 (米)与注水时间
(米)与注水时间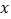 (小时)之间的函数关系式;
(小时)之间的函数关系式;(3)求注水多长时间时,甲、乙两个蓄水池中水的深度相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角. 其中正确的是 (填序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市扶贫办在精准扶贫工作中,组织30辆汽车装运花椒、核桃、甘蓝向外地销售.按计划30辆车都要装运,每辆汽车只能装运同一种产品,且必须装满,根据下表提供的信息,解答以下问题:
产品名称
核桃
花椒
甘蓝
每辆汽车运载量(吨)
10
6
4
每吨土特产利润(万元)
0.7
0.8
0.5
若装运核桃的汽车为x辆,装运甘蓝的车辆数是装运核桃车辆数的2倍多1,假设30辆车装运的三种产品的总利润为y万元.
(1)求y与x之间的函数关系式;
(2)若装花椒的汽车不超过8辆,求总利润最大时,装运各种产品的车辆数及总利润最大值.
相关试题

